【题目】如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.
(1)请在图中画出平移后的△A′B′C′,
(2)再在图中画出△A′B′C′的高C′D′,并求出△ABC在整个平移过程中线段AC扫过的面积为________.
(3)能使S△MBC=S△ABC的格点M共有_______个(点M异于点A)

参考答案:
【答案】(1)见解析;(2)作图见解析;32;(3)4.
【解析】
(1)分别将点A、B、C向左平移2格,再向上平移4格,得到点A′、B′、C′,然后顺次连接;
(2)过点C′作C′D′⊥A′B′的延长线于点D′即可,利用分割法即可求出线段AC扫过的面积;
(3)利用平行线的性质过点A作出BC的平行线进而得出符合题意的点.
解:(1)如图所示:△A′B′C′即为所求;
(2)如图所示:C′D′即为所求;
线段AC扫过的面积为:![]() ,
,
故答案为:32;

(3)如图所示:能使S△MBC=S△ABC的格点M的个数有4个.
故答案为:4.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2﹣2ax+c(a≠0)交x轴于A,B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.

(1)求抛物线的解析式;
(2)抛物线的对称轴l在边OA(不包括O、A两点)上平行移动,分别交x轴于点E,交CD于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM的长;
(3)在(2)的条件下,连结PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似?若存在,求出此时m的值,并直接判断△PCM的形状;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠A=20°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=74°,则原三角形的∠C的度数为( )

A.27°B.59°C.69°D.79°
-
科目: 来源: 题型:
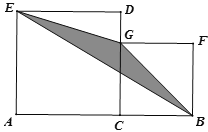
查看答案和解析>>【题目】如图,点C是线段AB上的一点,分别以AC.BC为边在AB的同侧作正方形ACDE和正方形CBFG,连接EG.BG.BE,当BC=1时,△BEG的面积记为S1,当BC=2时,△BEG的面积记为S2,……,以此类推,当BC=n时,△BEG的面积记为Sn,则S2020-S2019的值为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
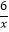 (x>0)的图象交于A(m,6),B(3,n)两点,与x轴交于点C,与y轴交于点D,下列结论:①一次函数解析式为y=﹣2x+8;②AD=BC;③kx+b﹣
(x>0)的图象交于A(m,6),B(3,n)两点,与x轴交于点C,与y轴交于点D,下列结论:①一次函数解析式为y=﹣2x+8;②AD=BC;③kx+b﹣ 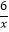 <0的解集为0<x<1或x>3;④△AOB的面积是8,其中正确结论的个数是( )
<0的解集为0<x<1或x>3;④△AOB的面积是8,其中正确结论的个数是( )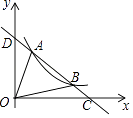
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,CD⊥AB,EF⊥AB,垂足分别为D、F.
(1)若∠1=∠2,试说明DG∥BC.
(2)若CD 平分∠ACB,∠A=60°,求∠B的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E,F分别在边CD,BC上,且∠EAF=45°,BD分别交AE,AF于点M,N,以点A为圆心,AB长为半径画弧BD.下列结论:①DE+BF=EF;②BN2+DM2=MN2;③△AMN∽△AFE;④
 与EF相切;⑤EF∥MN.其中正确结论的个数是( )
与EF相切;⑤EF∥MN.其中正确结论的个数是( )
A.5个
B.4个
C.3个
D.2个
相关试题

