搜索
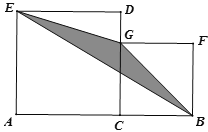
【题目】如图，点C是线段AB上的一点，分别以AC．BC为边在AB的同侧作正方形ACDE和正方形CBFG，连接EG．BG．BE，当BC＝1时，△BEG的面积记为S1，当BC＝2时，△BEG的面积记为S2，……，以此类推，当BC＝n时，△BEG的面积记为Sn，则S2020－S2019的值为____．
参考答案：
【答案】
【解析】
作辅助线，构建同底等高三角形，根据等腰直角三角形面积公式可得结论．
解：如图，连接EC，
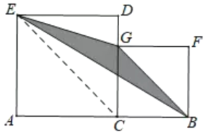
∵正方形ACDE和正方形CBFG，
∴∠ACE＝∠ABG＝45°，
∴EC∥BG，
∴△BCG和△BEG是同底（BG）等高的三角形，
即S△BCG＝S△BEG，
∴当BC＝n时，Sn＝
n2，
∴S2020S2019＝×20202×20192＝（2020＋2019）（20202019）＝；
故答案为：．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图1，a∥b，则∠1+∠2=
（2）如图2，AB∥CD，则∠1+∠2+∠3= ，并说明理由
（3）如图3，a∥b，则∠1+∠2+∠3+∠4=
（4）如图4，a∥b，根据以上结论，试探究∠1+∠2+∠3+∠4+…+∠n= （直接写出你的结论，无需说明理由）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=ax2﹣2ax+c（a≠0）交x轴于A，B两点，A点坐标为（3，0），与y轴交于点C（0，4），以OC、OA为边作矩形OADC交抛物线于点G．
（1）求抛物线的解析式；
（2）抛物线的对称轴l在边OA（不包括O、A两点）上平行移动，分别交x轴于点E，交CD于点F，交AC于点M，交抛物线于点P，若点M的横坐标为m，请用含m的代数式表示PM的长；
（3）在（2）的条件下，连结PC，则在CD上方的抛物线部分是否存在这样的点P，使得以P、C、F为顶点的三角形和△AEM相似？若存在，求出此时m的值，并直接判断△PCM的形状；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，∠A＝20°，沿BE将此三角形对折，又沿BA′再一次对折，点C落在BE上的C′处，此时∠C′DB＝74°，则原三角形的∠C的度数为（ ）
A.27°B.59°C.69°D.79°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上．将△ABC向左平移2格，再向上平移4格．
（1）请在图中画出平移后的△A′B′C′，
（2）再在图中画出△A′B′C′的高C′D′，并求出△ABC在整个平移过程中线段AC扫过的面积为________．
（3）能使S△MBC=S△ABC的格点M共有_______个（点M异于点A）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y=kx+b与反比例函数y=
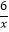（x＞0）的图象交于A（m，6），B（3，n）两点，与x轴交于点C，与y轴交于点D，下列结论：①一次函数解析式为y=﹣2x+8；②AD=BC；③kx+b﹣ 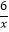＜0的解集为0＜x＜1或x＞3；④△AOB的面积是8，其中正确结论的个数是（ ）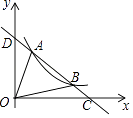
A.4个
B.3个
C.2个
D.1个 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC 中，CD⊥AB，EF⊥AB，垂足分别为D、F．
（1）若∠1=∠2，试说明DG∥BC．
（2）若CD 平分∠ACB，∠A=60°，求∠B的度数．
相关试题
