搜索
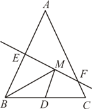
【题目】如图，等腰三角形ABC的底边BC的长为4，面积是12，腰AB的垂直平分线EF分别交AB、AC于点E、F，若点D为底边BC的中点，点M为线段EF上一动点，则△BDM的周长的最小值为_____．
参考答案：
【答案】8
【解析】
连接AD交EF与点M′，连结AM，由线段垂直平分线的性质可知AM=MB，则BM+DM=AM+DM，故此当A、M、D在一条直线上时，MB+DM有最小值，然后依据要三角形三线合一的性质可证明AD为△ABC底边上的高线，依据三角形的面积为12可求得AD的长．
解：连接AD交EF与点M′，连结AM．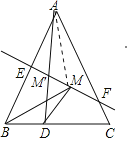
∵△ABC是等腰三角形，点D是BC边的中点，
∴AD⊥BC，
∴S△ABC=
BCAD=×4×AD=12，解得AD=6，
∵EF是线段AB的垂直平分线，
∴AM=BM．
∴BM+MD=MD+AM．
∴当点M位于点M′处时，MB+MD有最小值，最小值6．
∴△BDM的周长的最小值为DB+AD=2+6=8．
故答案为8.
-
科目： 来源： 题型：
查看答案和解析>>【题目】推理填空
已知，如图，
∥
，
∥
，
平分
交于
，
平分
交于
，求证:∥
证明:∵
∥∴
__________
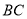
(两直线平行，同旁内角互补)∵
∥∴
__________(两直线平行，同旁内角互补)∴_____________=________________
又∵
平分∴____________
(角平分线定义)又∵
平分∴____________
(角平分线定义)∴_____________=________________
∵
∥∴
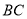
___________(两直线平行，内错角相等)∴_____________=________________(等量代换)
∴
∥(同位角相等，两直线平行) -
科目： 来源： 题型：
查看答案和解析>>【题目】小东家与学校之间是一条笔直的公路，早饭后，小东歩行前往学校，途中发现忘带画板，停下给妈妈打电话，妈妈接到电话后，带上画板马上赶往学校，同时小东沿原路返回，两人相遇后，小东立即赶往学校，妈妈沿原路返回，
时到家，假设小东始终以
的速度步行，两人离家的距离
(单位:
)与小东打完电话后的步行时间
(单位:
)之间的函数关系如图所示:
(1)小东打电话时，他离家__________
.(2)在图中的空格中，填上相应的数据.
(3)小东和妈妈相遇后，妈妈回家的速度为_________
.(4)_____________
时，两人相距
. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知等腰直角
和等腰直角
如图放置，
，
，
，其中，
、
、
在一条直线上，连接
并延长交
于
，
(1)求证:
(2)
与有什么位置关系？请说明理由.(3)若
，与
有什么数量关系？请说明理由. -
科目： 来源： 题型：
查看答案和解析>>【题目】对于一个两位数，十位数字是
，个位数字是
，总有
，我们把十位上的数与个位上的数的平方和叫做这个两位数的“平方和数”，把十位上的数与个位上的数的平方差叫做“平方差数”。例如，对两位数43来说，
，
，所以25和7分别是43的“平方和数”与“平方差数”。(1)76的“平方和数”是_____________，“平万差数”是____________.
(2)5可以是___________的“平方差数”.
(3)若一个数的“平方和数”是10，“平方差数”是8，则这个数是______.
(4)若一个数的“平方和数”，与它的“平方差数”相等，那么这个数满足什么特征？为什么？(写出说明过程)
(5)若一个数的“平方差数”等子它十位上的数与个位上的数差的十倍，此时，我们把它叫做“凑整数”，请你写出两个这样的凑整数_____________，__________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知:如图，等腰
中，
，
∥
，CD∥
，点
沿着
从
向
运动，同时点
沿着
从向
运动，、两点速度相同，当到达时，两点停止运动.
(1)图中有__________对全等三角形.请你找一对说明理由，写出过程.
(2)在
、运动过程中，图中阴影部分的面积是否发生变化？请说明理由.(3)当
平分
时，延长
交于
，试说明
.(4)在(3)的条件下，若
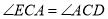，请问此时点和点重合吗?为什么? -
科目： 来源： 题型：
查看答案和解析>>【题目】在
和
中，
.点
在
上，BC、ED相交于点F，FE=FC，AB=DC，CF平分∠ACE.
（1）
与
相等吗？请说明理由；（2）请说明
是中点的理由.
相关试题
