【题目】对于一个两位数,十位数字是![]() ,个位数字是
,个位数字是![]() ,总有
,总有![]() ,我们把十位上的数与个位上的数的平方和叫做这个两位数的“平方和数”,把十位上的数与个位上的数的平方差叫做“平方差数”。例如,对两位数43来说,
,我们把十位上的数与个位上的数的平方和叫做这个两位数的“平方和数”,把十位上的数与个位上的数的平方差叫做“平方差数”。例如,对两位数43来说,![]() ,
,![]() ,所以25和7分别是43的“平方和数”与“平方差数”。
,所以25和7分别是43的“平方和数”与“平方差数”。
(1)76的“平方和数”是_____________,“平万差数”是____________.
(2)5可以是___________的“平方差数”.
(3)若一个数的“平方和数”是10,“平方差数”是8,则这个数是______.
(4)若一个数的“平方和数”,与它的“平方差数”相等,那么这个数满足什么特征?为什么?(写出说明过程)
(5)若一个数的“平方差数”等子它十位上的数与个位上的数差的十倍,此时,我们把它叫做“凑整数”,请你写出两个这样的凑整数_____________,__________.
参考答案:
【答案】(1)85,13;(2)32;(3)31;(4)这个数满足个位是0的特征,理由见解析;(5)55,91.
【解析】
(1)根据“平方和数”,“平方差数”的定义即可求解;
(2)找到两个平方数的差是5的数即可求解;
(3)先把“平方和数”加上“平方差数”,除以2后再求算术平方根可得十位上的数字,进一步可得个位上的数字;
(4)根据“平方和数”与“平方差数”相等,列式计算可得个位数字是0,依此即可求解;
(5)根据“凑整数”的定义列出方程,进一步得到满足条件的数即可求解.
解:(1)76的“平方和数”是72+62=85,“平方差数”是7262=13;
(2)因为3222=5,
所以5可以是,32的“平方差数”;
(3)(10+8)÷2=9,![]() =3,
=3,![]() =1,
=1,
故这个数是31;
(4)若一个数的“平方和数”与它的“平方差数”相等,那么这个数满足个位是0的特征,
理由:因为a2+b2=a2b2,
解得:b=0;
(5)依题意有a2b2=10(ab),
∴(ab)(a+b10)=0,
∴ab=0或a+b10=0.
因为a≥b,
则写出两个这样的凑整数为:55,91.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小东家与学校之间是一条笔直的公路,早饭后,小东歩行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回,
 时到家,假设小东始终以
时到家,假设小东始终以 的速度步行,两人离家的距离
的速度步行,两人离家的距离 (单位:
(单位: )与小东打完电话后的步行时间
)与小东打完电话后的步行时间 (单位:
(单位: )之间的函数关系如图所示:
)之间的函数关系如图所示:
(1)小东打电话时,他离家__________
 .
.(2)在图中的空格中,填上相应的数据.
(3)小东和妈妈相遇后,妈妈回家的速度为_________
 .
.(4)_____________
 时,两人相距
时,两人相距 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰直角
 和等腰直角
和等腰直角 如图放置,
如图放置, ,
, ,
, ,其中,
,其中, 、
、 、
、 在一条直线上,连接
在一条直线上,连接 并延长交
并延长交 于
于 ,
,
(1)求证:

(2)
 与
与 有什么位置关系?请说明理由.
有什么位置关系?请说明理由.(3)若
 ,
, 与
与 有什么数量关系?请说明理由.
有什么数量关系?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC的底边BC的长为4,面积是12,腰AB的垂直平分线EF分别交AB、AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为_____.
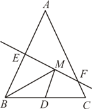
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,等腰
 中,
中, ,
, ∥
∥ ,CD∥
,CD∥ ,点
,点 沿着
沿着 从
从 向
向 运动,同时点
运动,同时点 沿着
沿着 从
从 向
向 运动,
运动, 、
、 两点速度相同,当
两点速度相同,当 到达
到达 时,两点停止运动.
时,两点停止运动.
(1)图中有__________对全等三角形.请你找一对说明理由,写出过程.
(2)在
 、
、 运动过程中,图中阴影部分的面积是否发生变化?请说明理由.
运动过程中,图中阴影部分的面积是否发生变化?请说明理由.(3)当
 平分
平分 时,延长
时,延长 交
交 于
于 ,试说明
,试说明 .
.(4)在(3)的条件下,若
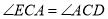 ,请问此时
,请问此时 点和
点和 点重合吗?为什么?
点重合吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】在
 和
和 中,
中, .点
.点 在
在 上,BC、ED相交于点F,FE=FC,AB=DC,CF平分∠ACE.
上,BC、ED相交于点F,FE=FC,AB=DC,CF平分∠ACE.
(1)
 与
与 相等吗?请说明理由;
相等吗?请说明理由;(2)请说明
 是
是 中点的理由.
中点的理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠C=120°,AD=4,AB=2,点H、G分别是边CD、BC上的动点.连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF则EF的最大值与最小值的差为__________.

相关试题

