【题目】推理填空
已知,如图,![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,
,![]() 平分
平分![]() 交
交![]() 于
于![]() ,
,![]() 平分
平分![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() ∥
∥![]()

证明:∵![]() ∥
∥![]()
∴![]() __________
__________![]() (两直线平行,同旁内角互补)
(两直线平行,同旁内角互补)
∵![]() ∥
∥![]()
∴![]() __________
__________![]() (两直线平行,同旁内角互补)
(两直线平行,同旁内角互补)
∴_____________=________________
又∵![]() 平分
平分![]()
∴____________![]() (角平分线定义)
(角平分线定义)
又∵![]() 平分
平分![]()
∴____________![]() (角平分线定义)
(角平分线定义)
∴_____________=________________
∵![]() ∥
∥![]()
∴![]() ___________(两直线平行,内错角相等)
___________(两直线平行,内错角相等)
∴_____________=________________(等量代换)
∴![]() ∥
∥![]() (同位角相等,两直线平行)
(同位角相等,两直线平行)
参考答案:
【答案】见解析.
【解析】
根据平行线的性质得出∠A+∠ABC=180°,∠A+∠ADC=180°,求出∠ABC=∠ADC,根据角平分线定义求出∠EBF=∠ADF,求出∠AEB=∠ADF即可.
证明:∵AD∥BC,
∴∠A+∠ABC=180°(两直线平行,同旁内角互补),
∵AB∥CD,
∴∠A+∠ADC=180°(两直线平行,同旁内角互补)
∴∠ABC=∠ADC,
又∵BE平分∠ABC,
∴∠EBF=![]() ∠ABC(角平分线定义),
∠ABC(角平分线定义),
又∵DF平分∠ADC
∴∠ADF=![]() ∠ADC(角平分线定义),
∠ADC(角平分线定义),
∴∠EBF=∠ADF,
∵AD∥BC,
∴∠AEB=∠EBF(两直线平行,内错角相等),
∴∠AEB=∠ADF(等量代换),
∴BE∥DP(同位角相等,两直线平行),
故答案为:∠ABC,∠ADC,∠ABC,∠ADC,∠EBF,∠ADF,∠EBF,∠ADF,∠EBF,∠AEB,∠ADF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F.
(1)求证:△AOE≌△COF;
(2)若∠EOD=30°,求CE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. “打开电视机,正在播放体育节目”是必然事件
B. 了解夏季冷饮市场上冰淇淋的质量情况适合用普查
C. 抛掷一枚普通硬币,“这枚硬币正面朝上”,这一事件发生的概率为
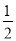
D. 甲、乙两人在相同条件下各射击10次,他们的成绩的平均数相同,方差分别是S甲2=0.3,S乙2=0.5,则乙的射击成绩较稳定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD 边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有( )

A. 4次 B. 3次 C. 2次 D. 1次
-
科目: 来源: 题型:
查看答案和解析>>【题目】小东家与学校之间是一条笔直的公路,早饭后,小东歩行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回,
 时到家,假设小东始终以
时到家,假设小东始终以 的速度步行,两人离家的距离
的速度步行,两人离家的距离 (单位:
(单位: )与小东打完电话后的步行时间
)与小东打完电话后的步行时间 (单位:
(单位: )之间的函数关系如图所示:
)之间的函数关系如图所示:
(1)小东打电话时,他离家__________
 .
.(2)在图中的空格中,填上相应的数据.
(3)小东和妈妈相遇后,妈妈回家的速度为_________
 .
.(4)_____________
 时,两人相距
时,两人相距 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰直角
 和等腰直角
和等腰直角 如图放置,
如图放置, ,
, ,
, ,其中,
,其中, 、
、 、
、 在一条直线上,连接
在一条直线上,连接 并延长交
并延长交 于
于 ,
,
(1)求证:

(2)
 与
与 有什么位置关系?请说明理由.
有什么位置关系?请说明理由.(3)若
 ,
, 与
与 有什么数量关系?请说明理由.
有什么数量关系?请说明理由. -
科目: 来源: 题型:
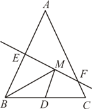
查看答案和解析>>【题目】如图,等腰三角形ABC的底边BC的长为4,面积是12,腰AB的垂直平分线EF分别交AB、AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为_____.
相关试题

