【题目】如图,在梯形ABCD中,已知AD∥BC,∠B=90°,AB=7,AD=9,BC=12,在线段BC上任取一点E,连接DE,作EF⊥DE,交直线AB于点F. 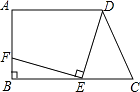
(1)若点F与B重合,求CE的长;
(2)若点F在线段AB上,且AF=CE,求CE的长.
参考答案:
【答案】
(1)解:当F和B重合时,
∵EF⊥DE,
∵DE⊥BC,
∵∠B=90°,
∴AB⊥BC,
∴AB∥DE,
∵AD∥BC,
∴四边形ABED是平行四边形,
∴AD=EF=9,
∴CE=BC﹣EF=12﹣9=3
(2)解:过D作DM⊥BC于M,
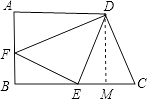
∵∠B=90°,
∴AB⊥BC,
∴DM∥AB,
∵AD∥BC,
∴四边形ABMD是矩形,
∴AD=BM=9,AB=DM=7,CM=12﹣9=3,
设AF=CE=a,则BF=7﹣a,EM=a﹣3,BE=12﹣a,
∵∠FEC=∠B=∠DMB=90°,
∴∠FEB+∠DEM=90°,∠BFE+∠FEB=90°,
∴∠BFE=∠DEM,
∵∠B=∠DME,
∴△FBE∽△EMD,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
a=5,a=17,
∵点F在线段AB上,AB=7,
∴AF=CE=17(舍去),
即CE=5.
【解析】(1)根据题意画出图形,得出矩形ABEC求出BE,即可求出CE;(2)过D作DM⊥BC于M,得出四边形ABMD是矩形,推出AD=BM=9,AB=DM=7,CM=12﹣9=3,设AF=CE=a,则BF=7﹣a,EM=a﹣3,BE=12﹣a,求出∠BFE=∠DEM,∠B=∠DME,证△FBE∽△EMD,得出比例式 ![]() =
= ![]() ,求出a即可.
,求出a即可.
【考点精析】本题主要考查了梯形的定义和相似三角形的判定与性质的相关知识点,需要掌握一组对边平行,另一组对边不平行的四边形是梯形.两腰相等的梯形是等腰梯形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A,与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
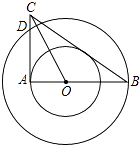
(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC、AD、BC之间的数量关系,并说明理由.
(3)若AB=8,BC=10,求大圆与小圆围成的圆环的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)15﹣(﹣8)+(﹣20)﹣12
(2)2×(﹣3)2﹣4×(﹣3)+15
(3)(﹣
 )2+|﹣2|3﹣
)2+|﹣2|3﹣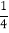
(4)﹣20+(﹣2)2﹣32+|﹣10|
(5)﹣22
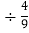 ×
×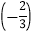 2
2 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙两辆汽车先后从A地出发到B地,甲车出发1小时后,乙车才出发,如图所示的l1和l2表示甲,乙两车相对于出发地的距离y(km)与追赶时间x(h)之间的关系:
(1)哪条线表示乙车离出发地的距离y与追赶时间x之间的关系?
(2)甲,乙两车的速度分别是多少?
(3)试分别确定甲,乙两车相对于出发地的距离y(km)与追赶时间x(h)之间的关系式;
(4)乙车能在1.5小时内追上甲车吗?若能,说明理由;若不能,求乙车出发几小时才能追上甲?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,点D,E分别是AB,BC上的点,且满足AC=DC=DE=BE=1,则tanA= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利情况如表所示:
销售方式
粗加工后销售
精加工后销售
每吨获利(元)
1000
2000
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工. ①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间? -
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
(1)请在数轴上标出下列各数,按从小到大的顺序排列,并用“<”号连接:
2,﹣2
 ,﹣
,﹣ ,0.5;
,0.5;
(2)有理数a、b在数轴上的位置如图所示:

化简:|a|= ,|﹣b|= ,|1+a|= ,|1﹣b|= .
相关试题

