【题目】甲,乙两辆汽车先后从A地出发到B地,甲车出发1小时后,乙车才出发,如图所示的l1和l2表示甲,乙两车相对于出发地的距离y(km)与追赶时间x(h)之间的关系:
(1)哪条线表示乙车离出发地的距离y与追赶时间x之间的关系?
(2)甲,乙两车的速度分别是多少?
(3)试分别确定甲,乙两车相对于出发地的距离y(km)与追赶时间x(h)之间的关系式;
(4)乙车能在1.5小时内追上甲车吗?若能,说明理由;若不能,求乙车出发几小时才能追上甲?

参考答案:
【答案】(1)l2表示乙车离出发地的距离y与追赶时间x之间的关系;(2)甲车的速度为60km/h,乙车的速度为90km/h;(3)y1=60x+60;y2=90x;(4)乙车不能在1.5小时内追上甲车.乙车追上甲车时,乙车行驶了2小时.
【解析】
(1)通过分析函数图象就可以得出l2表示B车离出发地的距离y与追赶时间x之间的关系;
(2)根据速度=路程÷时间就可以求出两车的速度;
(3)根据题意得出函数关系式即可;
(4)设B车行驶a小时可以追上A车,由追击问题的等量关系建立方程求出其解;
(1)由函数图象,得
l2表示乙车离出发地的距离y与追赶时间x之间的关系;
(2)甲车的速度为![]() =60km/h,乙车的速度为
=60km/h,乙车的速度为![]() =90km/h;
=90km/h;
(3)甲车的函数的关系式为:y1=60x+60;
乙车的函数关系式为:y2=90x;
(4)设乙车行驶a小时可以追上甲车,由题意,得
90a=60+60a,
解得:a=2,
∵1.5<2,
∴乙车不能在1.5小时内追上甲车,乙车追上甲车时,乙车行驶了2小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了解学生的课外阅读情况,就“我最喜爱的课外读物”从文学、艺术、科普和其它四个类别进行了抽样调查(每位同学仅选一项),并根据调查结果制作了尚不完整的频数分布表:
类别
频数(人数)
频率
文学
m
0.42
艺术
22
0.11
科普
66
n
其他
28
合计
1
(1)表中m= , n=;
(2)在这次抽样调查中,最喜爱阅读哪类读物的学生最少?
(3)根据以上调查,试估计该校1200名学生中最喜爱阅读科普读物的学生有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A,与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
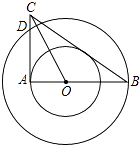
(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC、AD、BC之间的数量关系,并说明理由.
(3)若AB=8,BC=10,求大圆与小圆围成的圆环的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)15﹣(﹣8)+(﹣20)﹣12
(2)2×(﹣3)2﹣4×(﹣3)+15
(3)(﹣
 )2+|﹣2|3﹣
)2+|﹣2|3﹣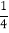
(4)﹣20+(﹣2)2﹣32+|﹣10|
(5)﹣22
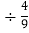 ×
×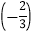 2
2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,已知AD∥BC,∠B=90°,AB=7,AD=9,BC=12,在线段BC上任取一点E,连接DE,作EF⊥DE,交直线AB于点F.
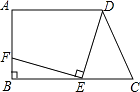
(1)若点F与B重合,求CE的长;
(2)若点F在线段AB上,且AF=CE,求CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,点D,E分别是AB,BC上的点,且满足AC=DC=DE=BE=1,则tanA= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利情况如表所示:
销售方式
粗加工后销售
精加工后销售
每吨获利(元)
1000
2000
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工. ①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
相关试题

