搜索
【题目】如图，在10×10的正方形网格中，每个小正方形的边长为1个单位长度．△ABC的顶点都在正方形网格的格点上，且通过两次平移（沿网格线方向作上下或左右平移）后得到△
，点C的对应点是直线上的格点
．
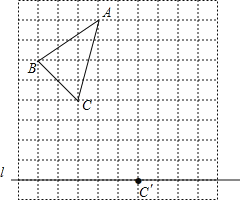
（1）画出△．
（2）若连接
、
，则这两条线段之间的关系是 ．
（3）试在直线
上画出所有符合题意的格点P，使得由点
、
、、P四点围成的四边形的面积为9．
参考答案：
【答案】（1）如图所示；见解析；（2）平行且相等；（3）如图所示；见解析．
【解析】
（1）根据图形平移的性质画出△A＇B＇C＇即可；
（2）图形平移得出AA＇,BB＇平行且相等；
（3）在直线上画出点P，使所组成的三角形面积相等即可．
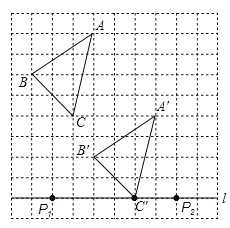
（1）如图所示：
（2）平行且相等；
（3）如图所示，P1,P2即为所求.
-
科目： 来源： 题型：
查看答案和解析>>【题目】将一副三角板如图摆放，∠OAB=∠OCD=90°，∠AOB=60°，∠COD=45°，OM平分∠AOD，ON平分∠COB，则∠MON的度数为（ ）
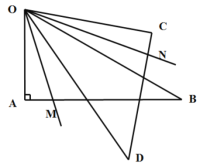
A.60°B.45°C.65.5°D.52.5°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，A(﹣1，5)，B(﹣1，0)，C(﹣4，3).
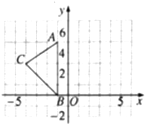
⑴请画出△ABC关于y轴对称的△A’B’C’(其中A’，B’，C’分別是A，B，C的对应点，不写画法)；
⑵直接写出A’，B’，C’三点的坐标：A’ ( )，B’( )，C’( )；
-
科目： 来源： 题型：
查看答案和解析>>【题目】无锡市旅游局为了亮化某景点，在两条笔直且互相平行的景观道MN、QP上分别放置A、B两盏激光灯，如图所示．A灯发出的光束自AM逆时针旋转至AN便立即回转；B灯发出的光束自BP逆时针旋转至BQ便立即回转，两灯不间断照射，A灯每秒转动30°，B灯每秒转动10°．B灯先转动2秒，A灯才开始转动．当B灯光束第一次到达BQ之前，两灯的光束互相平行时A灯旋转的时间是______秒．
-
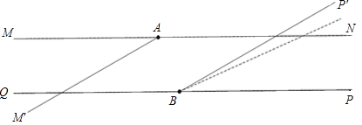
科目： 来源： 题型：
查看答案和解析>>【题目】完全平方公式：（a±b）2＝a2±2ab+b2适当的变形，可以解决很多的数学问题．
例如：若a+b＝3，ab＝1，求a2+b2的值．
解：因为a+b＝3，ab＝1
所以（a+b）2＝9，2ab＝2
所以a2+b2+2ab＝9，2ab＝2
得a2+b2＝7
根据上面的解题思路与方法，解决下列问题：
（1）若（7﹣x）（x﹣4）＝1，求（7﹣x）2+（x﹣4）2的值；
（2）如图，点C是线段AB上的一点，以AC、BC为边向两边作正方形，设AB＝5，两正方形的面积和S1+S2＝17，求图中阴影部分面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，∠BAC＝90°，点D是BC上一点，将△ABD沿AD翻折后得到△AED，边AE交射线BC于点F．（友情提醒：翻折前后的两个三角形的对应边相等，对应角相等．）
（1）如图①，当AE⊥BC时，求证：DE∥AC．
（2）若
，∠BAD＝x° ．①如图②，当DE⊥BC时，求x的值；
②是否存在这样的x的值，使得△DEF中有两个角相等．若存在，并求x的值；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校在艺术节宣传活动中，采用了四种宣传形式：A唱歌，B舞蹈，C朗诵，D器乐．全校的每名学生都选择了一种宣传形式参与了活动，小明对同学们选用的宣传形式，进行了随机抽样调查，根据调查统计结果，绘制了如图两种不完整的统计图表：
选项
方式
百分比
A
唱歌
35%
B
舞蹈
a
C
朗诵
25%
D
器乐
30%
请结合统计图表，回答下列问题：
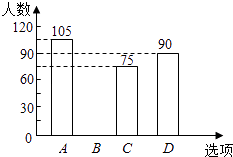
（1）本次调查的学生共人，a= ， 并将条形统计图补充完整 ；
（2）如果该校学生有2000人，请你估计该校喜欢“唱歌”这种宣传形式的学生约有多少人？
（3）学校采用调查方式让每班在A、B、C、D四种宣传形式中，随机抽取两种进行展示，请用树状图或列表法，求某班抽到的两种形式有一种是“唱歌”的概率．
相关试题
