【题目】在△ABC中,∠BAC=90°,点D是BC上一点,将△ABD沿AD翻折后得到△AED,边AE交射线BC于点F.(友情提醒:翻折前后的两个三角形的对应边相等,对应角相等.)



(1)如图①,当AE⊥BC时,求证:DE∥AC.
(2)若![]() ,∠BAD=x° .
,∠BAD=x° .
①如图②,当DE⊥BC时,求x的值;
②是否存在这样的x的值,使得△DEF中有两个角相等.若存在,并求x的值;若不存在,请说明理由.
参考答案:
【答案】(1)见解析;(2)①![]() ,②存在,
,②存在,![]() 或
或![]() .
.
【解析】
(1)根据折叠的性质得到∠B=∠E,根据平行线的判定定理证明;
(2)①根据三角形内角和定理分别求出∠C=60°,∠B=30°,根据折叠的性质计算即可;②分∠EDF=∠DFE、∠DFE=∠E、∠EDF=∠E三种情况,列方程解答即可.
(1)∵AE⊥BC
∴∠EAC+∠C=90°
∵∠BAC=90°
∴∠B+∠C=90°
∴∠B=∠EAC
∵将△ABD沿AD翻折后得到△AED
∴∠B=∠E
∴∠EAC=∠E
∴DE∥AC
(2)①∵∠B+∠C=90°,![]()
∴∠B=40°,∠C=50°
∵DE⊥BC
∴∠EDF=90°
∵将△ABD沿AD翻折后得到△AED
∴∠B=∠E=40°,∠BAD=∠EAD=![]() °
°
∴∠DFE=50°
∵∠DFE=![]()
∴![]()
∴![]()
②由题意可得,∠ADC=![]() , ∠ABD=
, ∠ABD=![]() ,
,
∠EDF=![]()
∠DFE=![]()
(ⅰ)若∠EDF=∠DFE ,可得![]() ,解得
,解得![]()
(ⅱ)若∠EDF=∠E ,可得![]() 解得
解得![]()
(ⅲ)若∠DFE =∠E,可得![]() 解得
解得![]() (舍去)
(舍去)
综上可得![]() 或
或![]() .
.
-
科目: 来源: 题型:
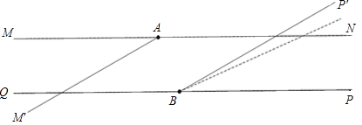
查看答案和解析>>【题目】无锡市旅游局为了亮化某景点,在两条笔直且互相平行的景观道MN、QP上分别放置A、B两盏激光灯,如图所示.A灯发出的光束自AM逆时针旋转至AN便立即回转;B灯发出的光束自BP逆时针旋转至BQ便立即回转,两灯不间断照射,A灯每秒转动30°,B灯每秒转动10°.B灯先转动2秒,A灯才开始转动.当B灯光束第一次到达BQ之前,两灯的光束互相平行时A灯旋转的时间是______秒.
-
科目: 来源: 题型:
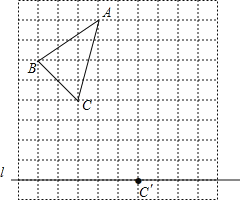
查看答案和解析>>【题目】如图,在10×10的正方形网格中,每个小正方形的边长为1个单位长度.△ABC的顶点都在正方形网格的格点上,且通过两次平移(沿网格线方向作上下或左右平移)后得到△
 ,点C的对应点是直线上的格点
,点C的对应点是直线上的格点 .
.
(1)画出△
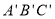 .
.(2)若连接
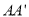 、
、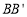 ,则这两条线段之间的关系是 .
,则这两条线段之间的关系是 .(3)试在直线
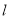 上画出所有符合题意的格点P,使得由点
上画出所有符合题意的格点P,使得由点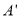 、
、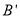 、
、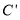 、P四点围成的四边形的面积为9.
、P四点围成的四边形的面积为9. -
科目: 来源: 题型:
查看答案和解析>>【题目】完全平方公式:(a±b)2=a2±2ab+b2适当的变形,可以解决很多的数学问题.
例如:若a+b=3,ab=1,求a2+b2的值.
解:因为a+b=3,ab=1
所以(a+b)2=9,2ab=2
所以a2+b2+2ab=9,2ab=2
得a2+b2=7
根据上面的解题思路与方法,解决下列问题:
(1)若(7﹣x)(x﹣4)=1,求(7﹣x)2+(x﹣4)2的值;
(2)如图,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=5,两正方形的面积和S1+S2=17,求图中阴影部分面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在艺术节宣传活动中,采用了四种宣传形式:A唱歌,B舞蹈,C朗诵,D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:
选项
方式
百分比
A
唱歌
35%
B
舞蹈
a
C
朗诵
25%
D
器乐
30%
请结合统计图表,回答下列问题:
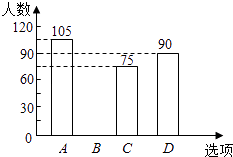
(1)本次调查的学生共人,a= , 并将条形统计图补充完整 ;
(2)如果该校学生有2000人,请你估计该校喜欢“唱歌”这种宣传形式的学生约有多少人?
(3)学校采用调查方式让每班在A、B、C、D四种宣传形式中,随机抽取两种进行展示,请用树状图或列表法,求某班抽到的两种形式有一种是“唱歌”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠C=90°,BE、DF分别平分∠ABC、∠ADC,判断BE、DF是否平行,并说明理由.
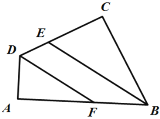
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AE是∠BAC的角平分线,AD是BC边上的高,且∠B = 40, ∠C = 60,求∠CAD、∠EAD的度数。(6分)
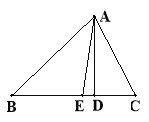
相关试题

