【题目】(1)计算:0×1×2×3+1=(_______)2;
1×2×3×4+1=(______)2;
2×3×4×5+1=(_______)2;
3×4×5×6+1=(_______)2;
……
(2)根据以上规律填空:4×5×6×7+1=(_____)2;
____×___×_____×_____+1=(55)2.
(3)小明说:“任意四个连续自然数的积与1的和都是某个奇数的平方”.你认为他的说法正确吗?请说明理由.
参考答案:
【答案】(1)1;5;11;19;(2)29;6;7;8;9;(3)正确,证明见解析.
【解析】
直接计算写出结果即可;
观察(1)的结果,得到规律,按照规律填写即可得到答案;
设四个自然数分别为n,n+1,n+2,n+3,按照题目意思作乘积,展开计算即可验证小明的说法;
解:(1)直接计算得到:0×1×2×3+1=1=12;
1×2×3×4+1=25=52;
2×3×4×5+1=121=112;
3×4×5×6+1=361=192;
故答案为:1;5;11;19;
(2)根据上述计算的几个式子,可以得到规律:
n(n+1)(n+2)(n+3)+1=![]() ,
,
∴4×5×6×7+1=![]() ,
,
∵![]() ,
,
∴ 6 × 7 × 8 × 9 +1=(55)2
故答案为:29,, 6 × 7 × 8 × 9
(3)正确, 理由如下:
证明:设四个自然数分别为n,n+1,n+2,n+3,
则有n(n+1)(n+2)(n+3)+1
=[n(n+3)][(n+1)(n+2)]+1
=(n2+3n)(n2+3n+2)+1
=(n2+3n)2+2(n2+3n)+1
=(n2+3n+1)2.
=[n(n+1)+2n+1]2
因为n为自然数,所以n(n+1)为偶数,2n+1为奇数,所以n(n+1)+2n+1必为奇数,故(n2+3n+1)2是一个奇数的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某家电商场计划用9万元从生产厂家购进50台电视机,已知该厂家生产3种不同型号的电视机,出厂价分别为A种每台1500元,B种每台2100元,C种每台2500元.
(1)若家电商场同时购进两种不同型号的电视机共50台,用去9万元,请你计算一下商场有哪几种进货方案?
(2)若商场销售一台A种电视机可获利150元,销售一台B种电视机可获利200元,销售一台C种电视机可获利250元,在同时购进两种不同型号的电视机方案中,为了使销售时获利最多,应选择哪种方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,∠ABC=90°,D为AC中点,点P是线段AD上的一点,点P与点A,点D不重合),连接BP.将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得到△A1B1P,连接A1B1、BB1
(1)如图①,当0°<α<90°,在α角变化过程中,请证明∠PAA1=∠PBB2 .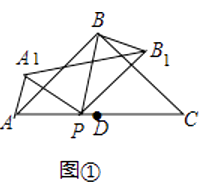
(2)如图②,直线AA1与直线PB、直线BB1分别交于点E,F.设∠ABP=β,当90°<α<180°时,在α角变化过程中,是否存在△BEF与△AEP全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;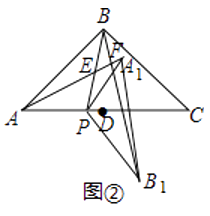
(3)如图③,当α=90°时,点E、F与点B重合.直线A1B与直线PB相交于点M,直线BB′与AC相交于点Q.若AB=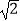 ,设AP=x,求y关于x的函数关系式.
,设AP=x,求y关于x的函数关系式.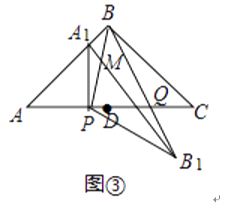
-
科目: 来源: 题型:
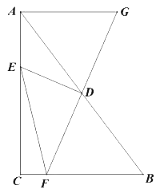
查看答案和解析>>【题目】如图,在△ABC中,D是边AB的中点,E是边AC上一动点,连结DE,过点D作DF⊥DE交边BC于点F(点F与点B、C不重合),延长FD到点G,使DG=DF,连结EF、AG.已知AB=10,BC=6,AC=8.
(1)求证:△ADG≌△BDF;
(2)请你连结EG,并求证:EF=EG;
(3)设AE=
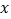 ,CF=
,CF= ,求
,求 关于
关于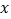 的函数关系式,并写出自变量
的函数关系式,并写出自变量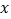 的取值范围;
的取值范围;(4)求线段EF长度的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)思考探究:如图,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,已知∠ABC=70°,∠ACD=100°.求∠A和∠P的度数.
(2)类比探究:如图,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,已知∠P=n°.求∠A的度数(用含n的式子表示).
(3)拓展迁移:已知,在四边形ABCD中,四边形ABCD的内角∠ABC与外角∠DCE的平分线所在直线相交于点P,∠P=n°,请画出图形;并探究出∠A+∠D的度数(用含n的式子表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)拼一拼,画一画:请你用4个长为a,宽为b的矩形拼成一个大正方形,并且正中间留下一个洞,这个洞恰好是一个小正方形。

(2)用不同方法计算中间的小正方形的面积,聪明的你能发现什么?
(3)当拼成的这个大正方形边长比中间小正方形边长多3cm时,它的面积就多24cm2,求中间小正方形的边长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,顶点为A的抛物线y=a(x+2)2﹣4交x轴于点B(1,0),连接AB,过原点O作射线OM∥AB,过点A作AD∥x轴交OM于点D,点C为抛物线与x轴的另一个交点,连接CD.

(1)求抛物线的解析式;
(2)若动点P从点O出发,以每秒1个单位长度的速度沿着射线OM运动,设点P运动的时间为t秒,问:当t为何值时,OB=AP;
(3)若动点P从点O出发,以每秒1个单位长度的速度沿线段OD向点D运动,同时动点Q从点C出发,以每秒2个单位长度的速度沿线段CO向点O运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动时间为t秒,连接PQ.问:当t为何值时,四边形CDPQ的面积最小?并求此时PQ的长.
相关试题

