【题目】(1)拼一拼,画一画:请你用4个长为a,宽为b的矩形拼成一个大正方形,并且正中间留下一个洞,这个洞恰好是一个小正方形。

(2)用不同方法计算中间的小正方形的面积,聪明的你能发现什么?
(3)当拼成的这个大正方形边长比中间小正方形边长多3cm时,它的面积就多24cm2,求中间小正方形的边长。
参考答案:
【答案】(1)如图所示;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】
本题用图象法验证两个完全平方公式之间的关系
(1)动手操作可发现外面大正方形的边长为a+b;里面小正方形的边长为(a-b);
(2)用整体法计算可得大正方形的面积为![]() ;采用部分相加的面积应为
;采用部分相加的面积应为![]() ,同样都是表示大正方形的面积,应相等;
,同样都是表示大正方形的面积,应相等;
(3)关系式为:大正方形的面积-小正方形的面积=24.
(1)如图,
 ;
;
(2)![]() ;
;
(3)设小正方形的边长为![]() x,
x,
由题意得,![]() ,
,
解的![]()
答:求中间小正方形的边长为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.
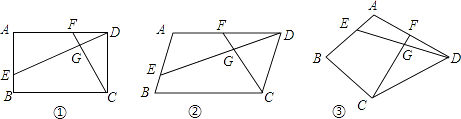
(1)如图①,若四边形ABCD是矩形,且DE⊥CF,求证:△ADE∽△DCF;
(2)如图②,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时,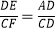 成立?并证明你的结论;
成立?并证明你的结论;
(3)如图③,若BA=BC=6,DA=DC=8,∠BAD=90°,DE⊥CF,请直接写出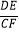 的值.
的值. -
科目: 来源: 题型:
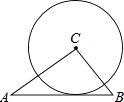
查看答案和解析>>【题目】如图,△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则⊙C的半径为( )
A.2.3
B.2.4
C.2.5
D.2.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
(1)如图1,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
(2)如图2,当EF与AB相交时,若∠EAB=α(0°<α<90°),请你直接写出线段EG、AG、BG之间的数量关系(用含α的式子表示);
(3)如图3,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小强的钱包内有10元钱、20元钱和50元钱的纸币各1张.
(1)若从中随机取出1张纸币,求取出纸币的金额是20元的概率;
(2)若从中随机取出2张纸币,求取出纸币的总额可购买一件51元的商品的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】宁波火车站北广场将于2015年底投入使用,计划在广场内种植A,B两种花木共6600棵,若A花木数量是B花木数量的2倍少600棵
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务? -
科目: 来源: 题型:
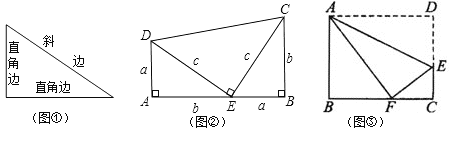
查看答案和解析>>【题目】我们已经知道,有一个内角是直角的三角形是直角三角形.其中直角所在的两条边叫直角边,直角所对的边叫斜边(如图①所示).数学家已发现在一个直角三角形中,两个直角边边长的平方和等于斜边长的平方.如果设直角三角形的两条直角边长度分别是
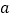 和
和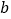 ,斜边长度是
,斜边长度是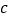 ,那么可以用数学语言表达:
,那么可以用数学语言表达: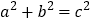 .
.
(1)在图②,若
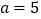 ,
,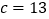 ,则
,则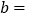 ;
;(2)观察图②,利用面积与代数恒等式的关系,试说明
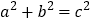 的正确性.其中两个相同的直角三角形边AE、EB在一条直线上;
的正确性.其中两个相同的直角三角形边AE、EB在一条直线上;(3)如图③所示,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8,BC=10,利用上面的结论求EF的长.
相关试题

