【题目】在△ABC中,AB=AC,∠ABC=90°,D为AC中点,点P是线段AD上的一点,点P与点A,点D不重合),连接BP.将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得到△A1B1P,连接A1B1、BB1
(1)如图①,当0°<α<90°,在α角变化过程中,请证明∠PAA1=∠PBB2 . 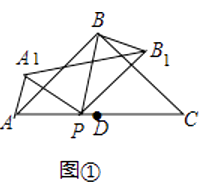
(2)如图②,直线AA1与直线PB、直线BB1分别交于点E,F.设∠ABP=β,当90°<α<180°时,在α角变化过程中,是否存在△BEF与△AEP全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;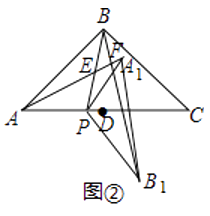
(3)如图③,当α=90°时,点E、F与点B重合.直线A1B与直线PB相交于点M,直线BB′与AC相交于点Q.若AB= ![]() ,设AP=x,求y关于x的函数关系式.
,设AP=x,求y关于x的函数关系式.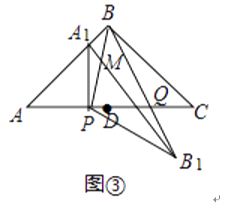
参考答案:
【答案】
(1)解:∵将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得到△A1B1P,
∴∠APA1=∠BPB1=α,AP=A1P,BP=B1P,
∴∠AA1P=∠A1AP= ![]() =
= ![]() ,∠BB1P=∠B1BP=
,∠BB1P=∠B1BP= ![]() =
= ![]() ,
,
∴∠PAA1=∠PBB1
(2)解:假设在α角变化的过程中,存在△BEF与△AEP全等,
∵△BEF与△AEP全等,
∴AE=BE,
∴∠ABE=∠BAE=β,
∵AP=A1P,
∴∠A1AP=∠AA1P= ![]() ,
,
∵AB=BC,∠ABC=90°,
∴∠BAC=45°,
∴β+ ![]() =45°,
=45°,
∴α﹣2β=90°
(3)解:当α=90°时,
∵AP=A1P,BP=B1P,∠APA1=∠BPB2=90°,
∴∠A=∠PBB1=45°,
∵∠A=∠C,∠AQB=∠C+∠QBC=45°+∠QBC=∠PBC,
∴△ABQ∽△CPB,
∴ ![]() ,
,
∵AB= ![]() ,
,
∴ ![]() ,
,
∴y= ![]()
【解析】(1)将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得到△A1B1P,根据旋转的性质得到对应角相等对应边相等,求∠PAA1=∠PBB2;(2)在α角变化的过程中,存在△BEF与△AEP全等,得到对应角相等对应边相等,根据三角形内角和定理求出α﹣2β的值;(3)当α=90°时,根据旋转的性质得到△ABQ∽△CPB,求出比例,得到AB的值,求出y关于x的函数关系式.
【考点精析】本题主要考查了函数关系式的相关知识点,需要掌握用来表示函数关系的数学式子叫做函数解析式或函数关系式才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P1、P2(P2在P1的右侧)是y=
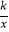 (k>0)在第一象限上的两点,点A1的坐标为(2,0).
(k>0)在第一象限上的两点,点A1的坐标为(2,0).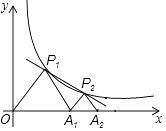
(1)填空:当点P1的横坐标逐渐增大时,△P1OA1的面积将(减小、不变、增大)
(2)若△P1OA1与△P2A1A2均为等边三角形,
①求反比例函数的解析式;
②求出点P2的坐标,并根据图象直接写在第一象限内,当x满足什么条件时,经过点P1、P2的一次函数的函数值大于反比例函数y=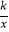 的函数值.
的函数值. -
科目: 来源: 题型:
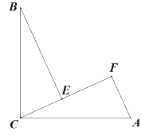
查看答案和解析>>【题目】如图,∠BCA=90°,AC=BC,BE⊥CF于点E,AF⊥CF于点F,其中0<∠ACF<45°.
(1)求证:△BEC≌△CEA;
(2)若AF=5,EF=8,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某家电商场计划用9万元从生产厂家购进50台电视机,已知该厂家生产3种不同型号的电视机,出厂价分别为A种每台1500元,B种每台2100元,C种每台2500元.
(1)若家电商场同时购进两种不同型号的电视机共50台,用去9万元,请你计算一下商场有哪几种进货方案?
(2)若商场销售一台A种电视机可获利150元,销售一台B种电视机可获利200元,销售一台C种电视机可获利250元,在同时购进两种不同型号的电视机方案中,为了使销售时获利最多,应选择哪种方案?
-
科目: 来源: 题型:
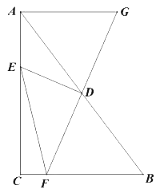
查看答案和解析>>【题目】如图,在△ABC中,D是边AB的中点,E是边AC上一动点,连结DE,过点D作DF⊥DE交边BC于点F(点F与点B、C不重合),延长FD到点G,使DG=DF,连结EF、AG.已知AB=10,BC=6,AC=8.
(1)求证:△ADG≌△BDF;
(2)请你连结EG,并求证:EF=EG;
(3)设AE=
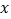 ,CF=
,CF= ,求
,求 关于
关于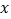 的函数关系式,并写出自变量
的函数关系式,并写出自变量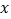 的取值范围;
的取值范围;(4)求线段EF长度的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:0×1×2×3+1=(_______)2;
1×2×3×4+1=(______)2;
2×3×4×5+1=(_______)2;
3×4×5×6+1=(_______)2;
……
(2)根据以上规律填空:4×5×6×7+1=(_____)2;
____×___×_____×_____+1=(55)2.
(3)小明说:“任意四个连续自然数的积与1的和都是某个奇数的平方”.你认为他的说法正确吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)思考探究:如图,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,已知∠ABC=70°,∠ACD=100°.求∠A和∠P的度数.
(2)类比探究:如图,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,已知∠P=n°.求∠A的度数(用含n的式子表示).
(3)拓展迁移:已知,在四边形ABCD中,四边形ABCD的内角∠ABC与外角∠DCE的平分线所在直线相交于点P,∠P=n°,请画出图形;并探究出∠A+∠D的度数(用含n的式子表示).

相关试题

