【题目】如图,顶点为A的抛物线y=a(x+2)2﹣4交x轴于点B(1,0),连接AB,过原点O作射线OM∥AB,过点A作AD∥x轴交OM于点D,点C为抛物线与x轴的另一个交点,连接CD.
(1)求抛物线的解析式;
(2)若动点P从点O出发,以每秒1个单位长度的速度沿着射线OM运动,设点P运动的时间为t秒,问:当t为何值时,OB=AP;
(3)若动点P从点O出发,以每秒1个单位长度的速度沿线段OD向点D运动,同时动点Q从点C出发,以每秒2个单位长度的速度沿线段CO向点O运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动时间为t秒,连接PQ.问:当t为何值时,四边形CDPQ的面积最小?并求此时PQ的长.
参考答案:
【答案】
(1)解:把(1,0)代入y=a(x+2)2﹣4,
得a= ![]() .
.
∴y= ![]() (x+2)2﹣4,
(x+2)2﹣4,
即y= ![]() x2+
x2+ ![]() x﹣
x﹣ ![]()
(2)解:由题意得OP=t,AB= ![]() =5,
=5,
若OB∥AP,即四边形ABOP为平行四边形时,OB=AP,且OP=AB=5,即当t=5时,OB=AP,
若OB不平行于AP,即四边形ABOP为等腰梯形时,OB=AP,连接AP,过点P作PG⊥AB,过点O作OH⊥AB,垂足分别为G、H,
∴△APG≌△BOH,
在Rt△OBM中,
∵OM= ![]() ,OB=1,
,OB=1,
∴BM= ![]() ,
,
∴OH= ![]() ,
,
∴BH= ![]() ,
,
∴OP=GH=AB﹣2BH= ![]() ,
,
即当t= ![]() 时,OB=AP
时,OB=AP
(3)解:将y=0代入y= ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() ,得
,得 ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() =0,
=0,
解得x=1或﹣5.
∴C(﹣5,0).
∴OC=5,
∵OM∥AB,AD∥x轴,
∴四边形ABOD是平行四边形,
∴AD=OB=1,
∴点D的坐标是(﹣3,﹣4),
∴S△DOC= ![]() ×5×4=10,
×5×4=10,
过点P作PN⊥BC,垂足为N.易证△OPN∽△BOH,

∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴PN= ![]() t,
t,
∴四边形CDPQ的面积S=S△DOC﹣S△OPQ=10﹣ ![]() ×(5﹣2t)×
×(5﹣2t)× ![]() t=
t= ![]() t2﹣2t+10,
t2﹣2t+10,
∴当t= ![]() 时,四边形CDPQ的面积S最小,
时,四边形CDPQ的面积S最小,
此时,点P的坐标是(﹣ ![]() ,﹣1),点Q的坐标是(﹣
,﹣1),点Q的坐标是(﹣ ![]() ,0),
,0),
∴PQ= ![]() =
= ![]() .
.
【解析】(1)把点B(1,0)代入抛物线的解析式,求出抛物线的解析式;(2)根据勾股定理求出AB的值,若OB∥AP,即四边形ABOP为平行四边形时,OB=AP,且OP=AB,当t=5时,OB=AP;若OB不平行于AP,即四边形ABOP为等腰梯形时,OB=AP,得到△APG≌△BOH,在Rt△OBM中,求出
BM![]() ,OH
,OH![]() ,BH
,BH![]() 的值,OP=GH=AB﹣2BH的值即可;(3)根据题意求出C的坐标,得到OC的值,由OM∥AB,AD∥x轴,得到四边形ABOD是平行四边形,AD=OB,求出点D的坐标,求出S△DOC的面积 ,证出△OPN∽△BOH,得到比例,求出PN的值,得到四边形CDPQ的面积S=S△DOC﹣S△OPQ,求出PQ的值;此题是综合题,难度较大,计算和解方程时需认真仔细.
的值,OP=GH=AB﹣2BH的值即可;(3)根据题意求出C的坐标,得到OC的值,由OM∥AB,AD∥x轴,得到四边形ABOD是平行四边形,AD=OB,求出点D的坐标,求出S△DOC的面积 ,证出△OPN∽△BOH,得到比例,求出PN的值,得到四边形CDPQ的面积S=S△DOC﹣S△OPQ,求出PQ的值;此题是综合题,难度较大,计算和解方程时需认真仔细.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:0×1×2×3+1=(_______)2;
1×2×3×4+1=(______)2;
2×3×4×5+1=(_______)2;
3×4×5×6+1=(_______)2;
……
(2)根据以上规律填空:4×5×6×7+1=(_____)2;
____×___×_____×_____+1=(55)2.
(3)小明说:“任意四个连续自然数的积与1的和都是某个奇数的平方”.你认为他的说法正确吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)思考探究:如图,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,已知∠ABC=70°,∠ACD=100°.求∠A和∠P的度数.
(2)类比探究:如图,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,已知∠P=n°.求∠A的度数(用含n的式子表示).
(3)拓展迁移:已知,在四边形ABCD中,四边形ABCD的内角∠ABC与外角∠DCE的平分线所在直线相交于点P,∠P=n°,请画出图形;并探究出∠A+∠D的度数(用含n的式子表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)拼一拼,画一画:请你用4个长为a,宽为b的矩形拼成一个大正方形,并且正中间留下一个洞,这个洞恰好是一个小正方形。

(2)用不同方法计算中间的小正方形的面积,聪明的你能发现什么?
(3)当拼成的这个大正方形边长比中间小正方形边长多3cm时,它的面积就多24cm2,求中间小正方形的边长。
-
科目: 来源: 题型:
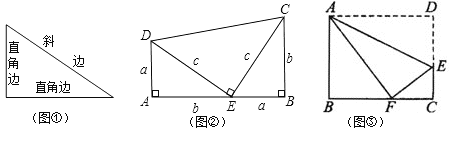
查看答案和解析>>【题目】我们已经知道,有一个内角是直角的三角形是直角三角形.其中直角所在的两条边叫直角边,直角所对的边叫斜边(如图①所示).数学家已发现在一个直角三角形中,两个直角边边长的平方和等于斜边长的平方.如果设直角三角形的两条直角边长度分别是
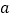 和
和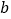 ,斜边长度是
,斜边长度是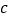 ,那么可以用数学语言表达:
,那么可以用数学语言表达: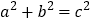 .
.
(1)在图②,若
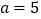 ,
,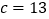 ,则
,则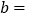 ;
;(2)观察图②,利用面积与代数恒等式的关系,试说明
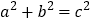 的正确性.其中两个相同的直角三角形边AE、EB在一条直线上;
的正确性.其中两个相同的直角三角形边AE、EB在一条直线上;(3)如图③所示,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8,BC=10,利用上面的结论求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】线段AB两端点坐标分别为A(
 ),B(
),B( ),现将它向右平移4个单位长度,向下平移2个单位长度,得到线段A1B1,则A1、B1的坐标分别为( )
),现将它向右平移4个单位长度,向下平移2个单位长度,得到线段A1B1,则A1、B1的坐标分别为( )A.A1(1,8),B1(-2,5)B.A1(3,2),B1(0,-1)
C.A1(-3,8),B1(-6,5)D.A1(-5,2),B1(-8,-1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列地方银行的标志中,既不是轴对称图形,也不是中心对称图形的是( )
A.
B.
C.
D.
相关试题

