Question

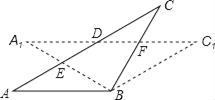
【题目】在△ABC中，AB=BC，将△ABC绕点B顺时针旋转α度，得到△A1BC1，A1B交AC于E，A1C1分别交AC、BC于点D、F，下列结论：①∠CDF=α，②A1E=CF，③DF=FC，④AD=CE，⑤A1F=CE．其中一定正确的有

A. ①②④ B. ②③④ C. ①②⑤ D. ③④⑤

Answer 1

【答案】C

【解析】

①两个不同的三角形中有两个角相等，那么第三个角也相等；

②根据ASA进而得出△A1BF≌△CBE，即可得出A1E=CF；

③∠CDF=α，而∠C与顺时针旋转的度数不一定相等，所以DF与FC不一定相等；

④AE不一定等于CD，则AD不一定等于CE，

⑤用角角边可证明△A1BF≌△CBE后可得A1F=CE．

∵△ABC绕点B顺时针旋转α度，得到△A1BC1，

∴∠CBC1=α，∠C=∠C1，

∵∠BFC1=∠DFC，

∴∠CDF=∠CBC1=α，故①正确，

∵AB=BC，

∴∠A=∠C，

∴∠C=∠A1

在△A1BF和△CBE中，

∠C=∠A1，A1B=BC，∠A1BF=∠CBE，

∴△A1BF≌△CBE，

∴BE=BF，A1F=CE，故⑤正确，

∵A1B=BC，

∴A1B-BE=BC-BF，即A1E=CF，故②正确，

∵∠CDF=α，α是可变化的角，∠C是固定角，

∴∠CDF不一定等于∠C，

∴DF不一定等于CF，故③错误，

∵AE不一定等于CD，

∴AD不一定等于CE，故④错误．

综上所述：①②⑤正确，

故选C.