【题目】如图,在Rt△ABO中,∠OBA=90°,AB=OB,点C在边AB上,且C(6,4),点D为OB的中点,点P为边OA上的动点,当∠APC=∠DPO时,点P的坐标为 ____.

参考答案:
【答案】(![]() ,
,![]() )
)
【解析】
根据题意,△ABO为等腰直角三角形,由点C坐标为(6,4),可知点B为(6,0),点A为(6,6),则直线OA为![]() ,作点D关于OA的对称点E,点E恰好落在y轴上,连接CE,交OA于点P,则点E坐标为(0,3),然后求出直线CE的解析式,联合
,作点D关于OA的对称点E,点E恰好落在y轴上,连接CE,交OA于点P,则点E坐标为(0,3),然后求出直线CE的解析式,联合![]() ,即可求出点P的坐标.
,即可求出点P的坐标.
解:在Rt△ABO中,∠OBA=90°,AB=OB,
∴△ABO是等腰直角三角形,
∵点C在边AB上,且C(6,4),
∴点B为(6,0),
∴OB=6=AB,
∴点A坐标为:(6,6),
∴直线OA的解析式为:![]() ;
;
作点D关于OA的对称点E,点E恰好落在y轴上,连接CE,交OA于点P,

∴∠APC=∠OPE=∠DPO,OD=OE,
∵点D是OB的中点,
∴点D的坐标为(3,0),
∴点E的坐标为:(0,3);
设直线CE的解析式为:![]() ,
,
把点C、E代入,得:![]() ,
,
解得:![]() ,
,
∴直线CE的解析式为:![]() ;
;
∴ ,解得:
,解得: ,
,
∴点P的坐标为:(![]() ,
,![]() );
);
故答案为:(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】从一副扑克牌中取出方块3、红心6、黑桃10共三张牌,洗匀后正面朝下放在桌面上,小明和小丽玩摸牌游戏,游戏规则如下:先由小明随机摸出一张牌,记下牌面数字后放回,洗匀后正面朝下,再由小丽随机摸出一张牌,记下牌面数字,这样记为一次游戏.当两人摸出的牌面数字不同时,牌面数字大的获胜;当两人摸出的牌面数字相同时,则视为平局.
(1)用画树状图或列表法,表示出小明、小丽两人一次游戏的所有可能的结果;
(2)求小明获胜的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】王强与李明两位同学在学习“概率”时,做抛骰子(正方体形状)试验,他们共抛了54次,出现向上点数的次数如下表:
向上点数
1
2
3
4
5
6
出现次数
6
9
5
8
16
10
(1)请计算出现向上点数为3的频率及出现向上点数为5的频率;
(2)王强说:“根据试验,可知一次试验中出现向上点数为5的概率最大.”李明说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”请判断王强和李明说法的对错.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△OAB的边长为2,以它的顶点O为原点,OB所在的直线为x轴,建立平面直角坐标系.若直线y=x+b与△OAB的边界总有两个公共点,则实数b的范围是____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(-4,-1),B(-5,-4),C(-1,-3).

(1)画△A'B'C',使△A'B'C'与△ABC关于y轴对称;
(2)在y轴上作一点P,使得PA+PC最短;
(3)将△ABC向右平移m个单位,向上平移n个单位,若点A落在第二象限内,且点C在第四象限内,则m的范围是 ,n的范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某所中学七、八、九年级各有6个班级,每个班级人数为50左右,根据实际情况,决定开设“A:乒乓球,B:篮球,C:跑步,D:跳绳”这四种项目.为了解学生喜欢哪一种项目,该学校体育组随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图和扇形统计图.请结合图中信息解答下列问题:
(1)样本容量是________,请你为体育组提供一种较为合理的抽样方案;
(2)把条形统计图补充完整;
(3)该校贝贝、晶晶、洋洋和妮妮是学校的校园之星,现要从这四人中选出两人作为“阳光体育”运动形象代言人,贝贝和晶晶同时被抽到的概率是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=BC,将△ABC绕点B顺时针旋转α度,得到△A1BC1,A1B交AC于E,A1C1分别交AC、BC于点D、F,下列结论:①∠CDF=α,②A1E=CF,③DF=FC,④AD=CE,⑤A1F=CE.其中一定正确的有
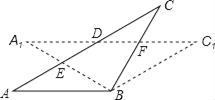
A. ①②④ B. ②③④ C. ①②⑤ D. ③④⑤
相关试题

