【题目】如图,在ABCD中,已知E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF. 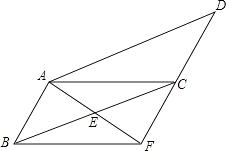
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.
参考答案:
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DF,
∴∠BAF=∠CFA.
∵E为BC的中点,
∴BE=CE.
在△AEB和△FEC中,
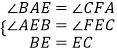 ,
,
∴△AEB≌△FEC(AAS)
∴AB=CF
(2)解:当BC=AF时,四边形ABFC是矩形,
理由:∵AB=CF,AB‖CF,
∴四边形ABFC是平行四边形,
∵BC=AF,
∴四边形ABFC是矩形.
【解析】(1)利用平行四边形的性质得出∠BAF=∠CFA,进而得出△AEB≌△FEC(AAS),求出答案;(2)首先得出四边形ABFC是平行四边形,进而得出答案.
【考点精析】通过灵活运用平行四边形的性质和矩形的判定方法,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图形的旋转只改变图形的_______,而不改变图形的_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,∠A=140°,∠D=80度.
(1)如图1,若∠B=∠C,试求出∠C的度数;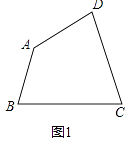
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;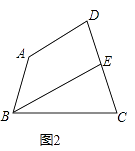
(3)如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.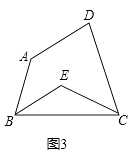
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形ABCD是矩形,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=4,DC=3,求BE的长.
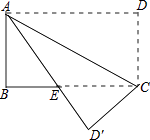
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a2a2=2a4B. (﹣a2)3=a4
C. 3a2﹣6a2=﹣3a2D. (a﹣3)2=a2﹣9
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解方程x2﹣2x﹣1=0,经过配方,得到( )
A.(x+1)2=3
B.(x﹣1)2=2
C.(x﹣1)2=3
D.(x﹣2)2=5 -
科目: 来源: 题型:
查看答案和解析>>【题目】动手操作: 如图①是一个长为2a,宽为2b的长方形,沿图中的虚线剪开分成四个大小相等的长方形,然后按照图②所示拼成一个正方形.
提出问题: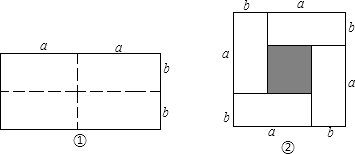
(1)观察图②,请用两种不同的方法表示阴影部分的面积;
(2)请写出三个代数式(a+b)2 , (a﹣b)2 , ab之间的一个等量关系. 问题解决:
根据上述(2)中得到的等量关系,解决下列问题:
已知:x+y=6,xy=3.求:(x﹣y)2的值.
相关试题

