【题目】如图所示,四边形ABCD是矩形,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=4,DC=3,求BE的长. 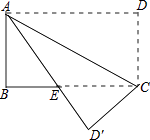
参考答案:
【答案】解:∵四边形ABCD为矩形, ∴AB=DC=3,BC=AD=4,AD∥BC,∠B=90°,
∵△ACD沿AC折叠到△ACD′,AD′与BC交于点E,
∴∠DAC=∠D′AC,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠D′AC=∠ACB,
∴AE=EC,
设BE=x,则EC=4﹣x,AE=4﹣x,
在Rt△ABE中,∵AB2+BE2=AE2 ,
∴32+x2=(4﹣x)2 , 解得x= ![]() ,
,
即BE的长为 ![]()
【解析】根据矩形性质得AB=DC=3,BC=AD=4,AD∥BC,∠B=90°,再根据折叠性质得∠DAC=∠D′AC,而∠DAC=∠ACB,则∠D′AC=∠ACB,所以AE=EC, 设BE=x,则EC=4﹣x,AE=4﹣x,然后在Rt△ABE中利用勾股定理可计算出BE.
【考点精析】解答此题的关键在于理解翻折变换(折叠问题)的相关知识,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. 2a2﹣a2=1B. (a2)3=a6C. a2+a3=a5D. (ab)2=ab2
-
科目: 来源: 题型:
查看答案和解析>>【题目】图形的旋转只改变图形的_______,而不改变图形的_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,∠A=140°,∠D=80度.
(1)如图1,若∠B=∠C,试求出∠C的度数;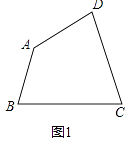
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;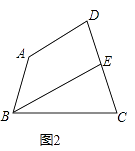
(3)如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.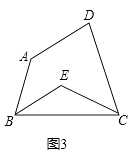
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,已知E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
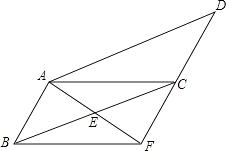
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a2a2=2a4B. (﹣a2)3=a4
C. 3a2﹣6a2=﹣3a2D. (a﹣3)2=a2﹣9
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解方程x2﹣2x﹣1=0,经过配方,得到( )
A.(x+1)2=3
B.(x﹣1)2=2
C.(x﹣1)2=3
D.(x﹣2)2=5
相关试题

