【题目】四边形ABCD中,∠A=140°,∠D=80度.
(1)如图1,若∠B=∠C,试求出∠C的度数; 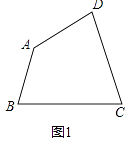
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数; 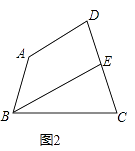
(3)如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数. 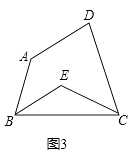
参考答案:
【答案】
(1)解:因为∠A+∠B+∠C+∠D=360,∠B=∠C,
所以∠B=∠C= ![]()
(2)解:∵BE∥AD,
∴∠BEC=∠D=80°,
∠ABE=180°﹣∠A=180°﹣140°=40°.
又∵BE平分∠ABC,
∴∠EBC=∠ABE=40°,
∴∠C=180°﹣∠EBC﹣∠BEC=180°﹣40°﹣80°=60°.
或解:∵BE∥AD,
∴∠ABE=180°﹣∠A=180°﹣140°=40°,
又∵BE平分∠ABC,
∴∠ABC=2∠ABE=80°,
∴∠C=360°﹣∠ABC﹣∠A﹣∠D=60°
(3)解:∵∠A+∠ABC+∠BCD+∠D=360°,
∴∠ABC+∠BCD=360°﹣∠A﹣∠D=360°﹣140°﹣80°=140°.
∵∠EBC= ![]() ∠ABC,∠BCE=
∠ABC,∠BCE= ![]() ∠BCD,
∠BCD,
∴∠E=180﹣∠EBC﹣∠BCE=180°﹣ ![]() (∠ABC+∠BCD)=180°﹣
(∠ABC+∠BCD)=180°﹣ ![]() ×140°=110°
×140°=110°
【解析】(1)根据四边形的内角和是360°,结合已知条件就可求解;(2)根据平行线的性质得到∠ABE的度数,再根据角平分线的定义得到∠ABC的度数,进一步根据四边形的内角和定理进行求解;(3)根据四边形的内角和定理以及角平分线的概念求得∠EBC+∠ECB的度数,再进一步求得∠BEC的度数.
【考点精析】解答此题的关键在于理解多边形内角与外角的相关知识,掌握多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:把△ABC沿AB边平移到△A′B′C′的位置,它们的重叠部分(即图中阴影部分)的面积是△ABC面积的一半,若AB=
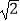 ,则此三角形移动的距离AA′是( )
,则此三角形移动的距离AA′是( ) 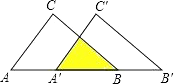
A.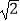 ﹣1
﹣1
B.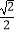
C.1
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. 2a2﹣a2=1B. (a2)3=a6C. a2+a3=a5D. (ab)2=ab2
-
科目: 来源: 题型:
查看答案和解析>>【题目】图形的旋转只改变图形的_______,而不改变图形的_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形ABCD是矩形,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=4,DC=3,求BE的长.
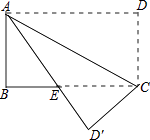
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,已知E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
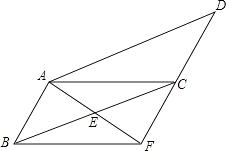
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a2a2=2a4B. (﹣a2)3=a4
C. 3a2﹣6a2=﹣3a2D. (a﹣3)2=a2﹣9
相关试题

