【题目】在菱形ABCD中,∠BAD=60°
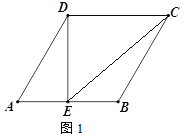
(1)如图1,点E为线段AB的中点,连接DE、CE,若AB=4,求线段EC的长;
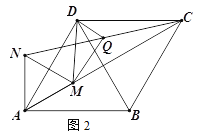
(2)如图2,M为线段AC上一点(不与A、C重合),以AM为边向上构造等边三角形AMN,连接NC、DM,Q为线段NC的中点,连接DQ、MQ,判断DM与DQ的数量关系,并证明你的结论.
参考答案:
【答案】(1)![]() ;(2)见解析;
;(2)见解析;
【解析】(1)连接DB,利用菱形的性质、等边三角形的性质及勾股定理即可求解;
(2)延长MQ到H,使QH=MQ,连接DH、HC ,利用全等三角形的判定和性质、菱形的性质、勾股定理等即可求解.
(1)∵菱形ABCD,
∴AD=DC=AB,DC∥AB,
∴∠DEA=∠CDE,
连接DB,
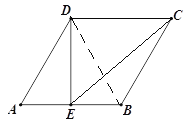
∵∠BAD=60°,
∴△ADB是等边三角形 ,
∵E为AB中点,
∴DE⊥AB,AE=![]() ,
,
∴∠DEA=90°,
∴∠CDE=90°,
在Rt△ADE中,AD=AB=4,AE=![]() =2,
=2,
∴DE=![]() ,
,
在Rt△DCE中,DC=AB=4,
∴EC=![]() ;
;
(2)延长MQ到H,使QH=MQ,连接DH、HC ,
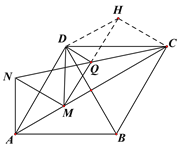
∵Q为NC中点,
∴NQ=CQ,
∵∠NQM=∠CQH,
∴△NQM≌△CQH(SAS),
∴NM=CH,∠MNQ=∠HCQ,
∴NM∥CH,
∴∠NMA=∠HCM,
∵有等边△AMN,
∴NM=AM,∠NMA=60°,
∴AM=CH,∠HCM=60°,
∵有菱形ABCD,AC为对角线,∠BAD=60°,
∴∠DAM=![]() ,
,
同理,∠DCA=30°,
∴∠HCD=30°,
∴△DAM≌△DCH(SAS),
∴DM=DH,∠ADM=∠CDH,
∴DQ⊥MH,∠MDQ=∠HDQ,∠MDH=∠ADC,
∴∠DQM=90°,
∵有菱形ABCD,∠BAD=60°,
∴∠ADC=120°,
∴∠MDH=120°,
∴∠MDQ=60°,
∴∠DMQ=30°,
∴DM=2DQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=Rt∠,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
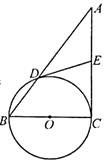
(1)求证:∠A=∠ADE;
(2)若AD=16,DE=10,求BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某活动中心准备带会员去龙潭大峡谷一日游,1张儿童票和2张成人票共需190元,2张儿童票和3张成人票共需300元.解答下列问题:
(1)求每张儿童票和每张成人票各多少元?
(2)这个活动中心想带50人去游玩,费用不超过3000元,并且出于安全考虑,儿童人数不能超过22人,请你帮助活动中心确立出游方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,∠A=30°,点P从点A出发以2cm/s的速度沿折线A—C—B运动,点Q从点A出发以a(cm/s)的速度沿AB运动,P,Q两点同时出发,当某一点运动到点B时,两点同时停止运动.设运动时间为x(s),△APQ的面积为y(cm2),y关于x的函数图象由C1 , C2两段组成,如图2所示.
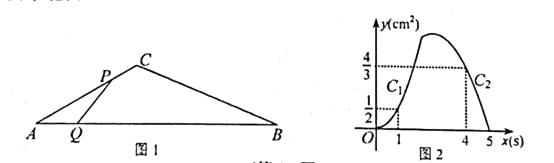
(1)求a的值;
(2)求图2中图象C2段的函数表达式;
(3)当点P运动到线段BC上某一段时△APQ的面积,大于当点P在线段AC上任意一点时△APQ的面积,求x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E是AD上的一个动点,连接BE,作点A关于BE的对称点F,且点F落在矩形ABCD的内部,连结AF,BF,EF,过点F作GF⊥AF交AD于点G,设
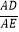 =n.
=n.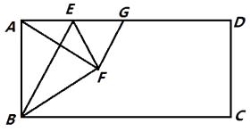
(1)求证:AE=GE;
(2)当点F落在AC上时,用含n的代数式表示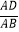 的值;
的值;
(3)若AD=4AB,且以点F,C,G为顶点的三角形是直角三角形,求n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E在BC的延长线上,则下列条件中,不能判定AB∥CD的是( )
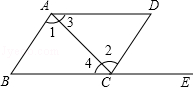
A.∠D+∠DAB=180°
B.∠B=∠DCE
C.∠1=∠2.
D.∠3=∠4 -
科目: 来源: 题型:
查看答案和解析>>【题目】光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台.现将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.
两地区与该农机租赁公司商定的每天的租赁价格见下表:

(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79600元,说明有多少种分派方案,并将各种方案设计出来;
(3)如何分派才能使这50台联合收割机每天获得的租金最高?
相关试题

