【题目】如图1,在△ABC中,∠A=30°,点P从点A出发以2cm/s的速度沿折线A—C—B运动,点Q从点A出发以a(cm/s)的速度沿AB运动,P,Q两点同时出发,当某一点运动到点B时,两点同时停止运动.设运动时间为x(s),△APQ的面积为y(cm2),y关于x的函数图象由C1 , C2两段组成,如图2所示.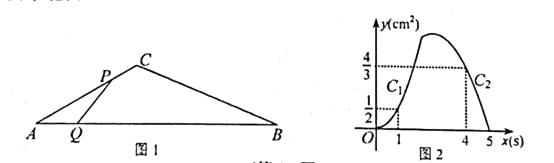
(1)求a的值;
(2)求图2中图象C2段的函数表达式;
(3)当点P运动到线段BC上某一段时△APQ的面积,大于当点P在线段AC上任意一点时△APQ的面积,求x的取值范围.
参考答案:
【答案】
(1)
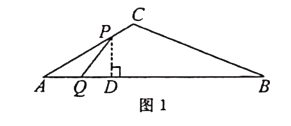
解:在图1中,过P作PD⊥AB于D,∵∠A=30°,PA=2x,
∴PD=PA·sin30°=2x· ![]() =x,
=x,
∴y= ![]() =
= ![]() .
.
由图象得,当x=1时,y= ![]() ,则
,则 ![]() =
= ![]() .
.
∴a=1.
(2)
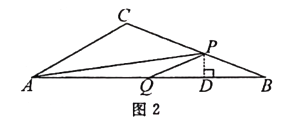
解:当点P在BC上时(如图2),PB=5×2-2x=10-2x.
∴PD=PB·sinB=(10-2x)·sinB,
∴y= ![]() AQ·PD=
AQ·PD= ![]() x·(10-2x)·sinB.
x·(10-2x)·sinB.
由图象得,当x=4时,y= ![]() ,
,
∴ ![]() ×4×(10-8)·sinB=
×4×(10-8)·sinB= ![]() ,
,
∴sinB= ![]() .
.
∴y= ![]() x·(10-2x)·
x·(10-2x)· ![]() =
= ![]() .
.
(3)
解:由C1,C2的函数表达式,得 ![]() =
= ![]() ,
,
解得x1=0(舍去),x2=2,
由图易得,当x=2时,函数y= ![]() 的最大值为y=
的最大值为y= ![]() .
.
将y=2代入函数y= ![]() ,得2=
,得2= ![]() .
.
解得x1=2,x2=3,
∴由图象得,x的取值范围是2<x<3.
【解析】(1)C1段的函数解析式是点P在AC线段时y与x的关系,由S= ![]() AQ·(AQ上的高),而AQ=ax,由∠A=30°,PA=2x,可过P作PD⊥AB于D,则PD=PA·sin30°=2x·
AQ·(AQ上的高),而AQ=ax,由∠A=30°,PA=2x,可过P作PD⊥AB于D,则PD=PA·sin30°=2x· ![]() =x,则可写出y关于x的解析式,代入点(1,
=x,则可写出y关于x的解析式,代入点(1, ![]() ),即可求出sinB,即可解答;(3)题中表示在某x的取值范围内C1<C2 , 即此时C2的y值大于C1的y值的最大值,由图易得,当x=2时,函数y=
),即可求出sinB,即可解答;(3)题中表示在某x的取值范围内C1<C2 , 即此时C2的y值大于C1的y值的最大值,由图易得,当x=2时,函数y= ![]() 的最大值为y=
的最大值为y= ![]() .将y=2代入函数y=
.将y=2代入函数y= ![]() ,求出x的值,根据函数y=
,求出x的值,根据函数y= ![]() ,的开口向下,则可得x的取值范围.
,的开口向下,则可得x的取值范围.
【考点精析】关于本题考查的二次函数的图象和二次函数的性质,需要了解二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能得出正确答案.
-
科目: 来源: 题型:
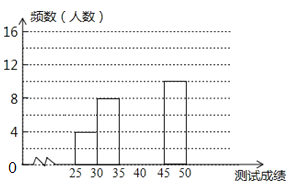
查看答案和解析>>【题目】为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别
成绩x分
频数(人数)
第1组
25≤x<30
4
第2组
30≤x<35
6
第3组
35≤x<40
14
第4组
40≤x<45
a
第5组
45≤x<50
10
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=Rt∠,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
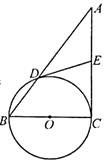
(1)求证:∠A=∠ADE;
(2)若AD=16,DE=10,求BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某活动中心准备带会员去龙潭大峡谷一日游,1张儿童票和2张成人票共需190元,2张儿童票和3张成人票共需300元.解答下列问题:
(1)求每张儿童票和每张成人票各多少元?
(2)这个活动中心想带50人去游玩,费用不超过3000元,并且出于安全考虑,儿童人数不能超过22人,请你帮助活动中心确立出游方案.
-
科目: 来源: 题型:
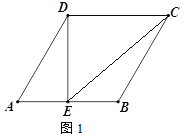
查看答案和解析>>【题目】在菱形ABCD中,∠BAD=60°
(1)如图1,点E为线段AB的中点,连接DE、CE,若AB=4,求线段EC的长;
(2)如图2,M为线段AC上一点(不与A、C重合),以AM为边向上构造等边三角形AMN,连接NC、DM,Q为线段NC的中点,连接DQ、MQ,判断DM与DQ的数量关系,并证明你的结论.
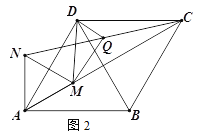
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E是AD上的一个动点,连接BE,作点A关于BE的对称点F,且点F落在矩形ABCD的内部,连结AF,BF,EF,过点F作GF⊥AF交AD于点G,设
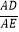 =n.
=n.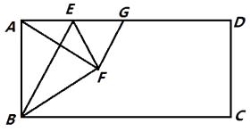
(1)求证:AE=GE;
(2)当点F落在AC上时,用含n的代数式表示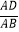 的值;
的值;
(3)若AD=4AB,且以点F,C,G为顶点的三角形是直角三角形,求n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E在BC的延长线上,则下列条件中,不能判定AB∥CD的是( )
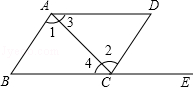
A.∠D+∠DAB=180°
B.∠B=∠DCE
C.∠1=∠2.
D.∠3=∠4
相关试题

