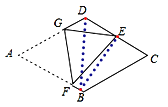
【题目】如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F,G分别在边AB,AD上,则EF的长为

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】A
【解析】分析: 连接BE,BD,如图,利用菱形的性质得△BDC为等边三角形,在Rt△BCE中计算出BE=![]() ,接着证明BE⊥AB, 利用折叠的性质得到EF=AF.,设EF=AF=x, FG垂直平分AE,所以在Rt△BEF中利用勾股定理列方程求解即可.
,接着证明BE⊥AB, 利用折叠的性质得到EF=AF.,设EF=AF=x, FG垂直平分AE,所以在Rt△BEF中利用勾股定理列方程求解即可.
详解: 连接BE,BD,如图,
∵四边形ABCD为菱形,∠A=60°,
∴△BDC为等边三角形, ∠C=∠A=60°,
∴∠CBE=90°-60°=30°.
∵E点为CD的中点,
∴CE=DE=1,BE⊥CD.
在Rt△BCE中,
BC=2CE=2,
BE=![]() .
.
∵AB∥CD,
∴BE⊥AB.
∵菱形纸片翻折,使点A落在CD的中点E处,
∴EF=AF.
设EF=AF=x,则BF=2-x,
在Rt△BEF中,
![]() ,
,
解得![]() .
.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系xOy中,等边△AOB的边长为6,点C在边OA上,点D在边AB上,且OC=3BD,反比例函数y=
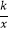 (k≠0)的图象恰好经过点C和点D,则k的值为( )
(k≠0)的图象恰好经过点C和点D,则k的值为( ) 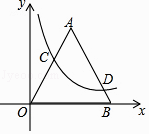
A.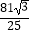
B.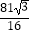
C.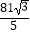
D.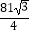
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如同,△ABC内接于⊙O,且半径OC⊥AB,点D在半径OB的延长线上,且∠A=∠BCD=30°,AC=2,则由
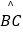 ,线段CD和线段BD所围成图形的阴影部分的面积为 .
,线段CD和线段BD所围成图形的阴影部分的面积为 . 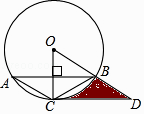
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在Rt△ACB中,∠ACB=90°,点D是AB的中点,点E是CD的中点,过点C作CF∥AB叫AE的延长线于点F.
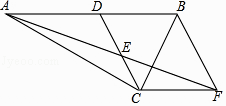
(1)求证:△ADE≌△FCE;
(2)若∠DCF=120°,DE=2,求BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为反比例函数
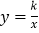 (x<0)在第三象限内图象上的一点,过点P分别作x轴、y轴的垂线交一次函数y=-x+4的图像于点A、B.若AO、BO分别平分∠BAP,∠ABP ,则k的值为___________.
(x<0)在第三象限内图象上的一点,过点P分别作x轴、y轴的垂线交一次函数y=-x+4的图像于点A、B.若AO、BO分别平分∠BAP,∠ABP ,则k的值为___________.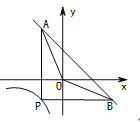
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列多面体,并把下表补充完整.
名称
三棱柱
四棱柱
五棱柱
六棱柱
图形
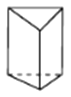
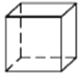
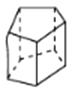
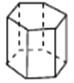
顶点数
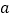
6
10
12
棱数
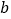
9
12
面数
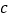
5
8
观察上表中的结果,你能发现
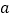 、
、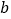 、
、之间有什么关系吗?请写出关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】荆岗中学决定在本校学生中,开展足球、篮球、羽毛球、乒乓球四种活动,为了了解学生对这四种活动的喜爱情况,学校随机调查了该校m名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图.
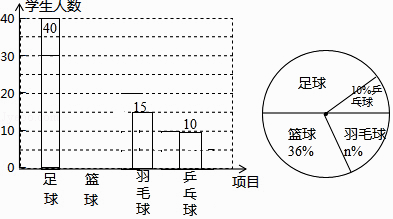
(1)m= , n=;
(2)请补全图中的条形图;
(3)根据抽样调查的结果,请估算全校1800名学生中,大约有多少人喜爱踢足球;
(4)在抽查的m名学生中,喜爱乒乓球的有10名同学(其中有4名女生,包括小红、小梅),现将喜爱打乒乓球的同学平均分成两组进行训练,且女生每组分两人,求小红、小梅能分在同一组的概率.
相关试题

