【题目】已知数轴上两点A、B所表示的数分别为a和b,且满足|a+3|+(b-9)2018=0,O为原点
(1) 试求a和b的值
(2) 点C从O点出发向右运动,经过3秒后点C到A点的距离是点C到B点距离的3倍,求点C的运动速度?
(3) 点D以1个单位每秒的速度从点O向右运动,同时点P从点A出发以5个单位每秒的速度向左运动,点Q从点B出发,以20个单位每秒的速度向右运动.在运动过程中,M、N分别为PD、OQ的中点,问![]() 的值是否发生变化,请说明理由.
的值是否发生变化,请说明理由.
参考答案:
【答案】(1) a=-3,b=9;(2)每秒5个单位或每秒2个单位;(3) ![]() 为定值,理由见解析
为定值,理由见解析
【解析】
(1) 根据非负数的和等于零,可得每个非负数同时为零,从而a=-3,b=9;
(2)设C点对应的数为x,CA=x-(-3)=x+3,由于点C存在在B点左侧和右侧两种情况,故CB的长为|x-9|,根据CA=3CB列式即可求出x,从而求得运动速度;
(3设运动时间为t秒,用含t的代数式分别表示PQ、OD、MN,然后代入![]() 求值即可判断.
求值即可判断.
(1) a=-3,b=9
(2) 设3秒后,点C对应的数为x
则CA=|x+3|,CB=|x-9|
∵CA=3CB
∴|x+3|=3|x-9|=|3x-27|
当x+3=3x-27,解得x=15,此时点C的速度为![]()
当x+3+3x-27=0,解得x=6,此时点C的速度为![]()
(3) 设运动的时间为t
点D对应的数为:t
点P对应的数为:-3-5t
点Q对应的数为:9+20t
点M对应的数为:-1.5-2t
点N对应的数为:4.5+10t
则PQ=25t+12,OD=t,MN=12t+6
∴![]() 为定值.
为定值.
故答案为:(1) a=-3,b=9;(2)每秒5个单位或每秒2个单位;(3) ![]() 为定值.
为定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=10,P是线段AB上的任意一点,在AB的同侧分别以AP、PB为边作等边三角形APC和等边三角形PBD,连结CD.
(1)当AP=6时,求CD的长;
(2)当AP为多少时,CD的值最小,最小值是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
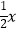 与双曲线y=
与双曲线y= 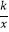 (k>0,x>0)交于点A,将直线y=
(k>0,x>0)交于点A,将直线y= 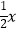 向上平移4个单位长度后,与y轴交于点C,与双曲线y=
向上平移4个单位长度后,与y轴交于点C,与双曲线y= 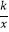 (k>0,x>0)交于点B,若OA=3BC,则k的值为( )
(k>0,x>0)交于点B,若OA=3BC,则k的值为( )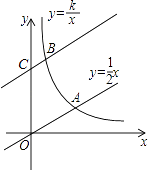
A.3
B.6
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】生活经验表明,靠墙摆放梯子时,若梯子底端离墙的距离约为梯子长度的
 ,则梯子比较稳定,如图,AB为一长度为6米的梯子.
,则梯子比较稳定,如图,AB为一长度为6米的梯子.(1)当梯子稳定摆放时,它的顶端能达到5.7米高的墙头吗?
(2)如图2,若梯子底端向左滑动(3
 ﹣2)米,那么梯子顶端将下滑多少米?
﹣2)米,那么梯子顶端将下滑多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为2的正三角形中,将其内切圆和三个角切圆(与角两边及三角形内切圆都相切的圆)的内部挖去,则此三角形剩下部分(阴影部分)的面积为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个定点坐标分别为A(﹣1,3),B(﹣1,1),C(﹣3,2).

(1)请画出△ABC关于y轴对称的△A1B1C1;
(2)以原点O为位似中心,将△A1B1C1放大为原来的2倍,得到△A2B2C2 , 请在第三象限内画出△A2B2C2 , 并求出 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=
 x+1与抛物线y=ax2+bx﹣3交于A,B两点,点A在x轴上,点B的纵坐标为3.点P是直线AB下方的抛物线上一动点(不与A,B重合),过点P作x轴的垂线交直线AB与点C,作PD⊥AB于点D
x+1与抛物线y=ax2+bx﹣3交于A,B两点,点A在x轴上,点B的纵坐标为3.点P是直线AB下方的抛物线上一动点(不与A,B重合),过点P作x轴的垂线交直线AB与点C,作PD⊥AB于点D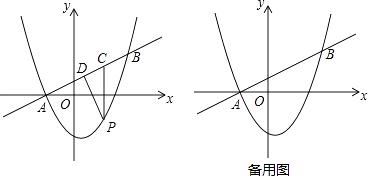
(1)①求抛物线的解析式;②求sin∠ACP的值
(2)设点P的横坐标为m
①用含m的代数式表示线段PD的长,并求出线段PD长的最大值;
②连接PB,线段PC把△PDB分成两个三角形,求出当这两个三角形面积之比为9:10时的m值;
③是否存在适合的m值,使△PCD与△PBD相似?若存在,直接写出m值;若不存在,说明理由.
相关试题

