【题目】如图,在平面直角坐标系中,直线y= ![]() x+1与抛物线y=ax2+bx﹣3交于A,B两点,点A在x轴上,点B的纵坐标为3.点P是直线AB下方的抛物线上一动点(不与A,B重合),过点P作x轴的垂线交直线AB与点C,作PD⊥AB于点D
x+1与抛物线y=ax2+bx﹣3交于A,B两点,点A在x轴上,点B的纵坐标为3.点P是直线AB下方的抛物线上一动点(不与A,B重合),过点P作x轴的垂线交直线AB与点C,作PD⊥AB于点D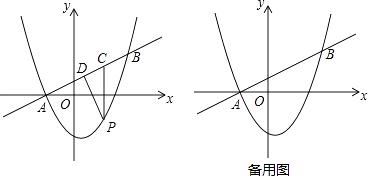
(1)①求抛物线的解析式;②求sin∠ACP的值
(2)设点P的横坐标为m
①用含m的代数式表示线段PD的长,并求出线段PD长的最大值;
②连接PB,线段PC把△PDB分成两个三角形,求出当这两个三角形面积之比为9:10时的m值;
③是否存在适合的m值,使△PCD与△PBD相似?若存在,直接写出m值;若不存在,说明理由.
参考答案:
【答案】
(1)
解:①当y=0时, ![]() x+1=0,解得x=﹣2,则A(﹣2,0),
x+1=0,解得x=﹣2,则A(﹣2,0),
当y=3时, ![]() x+1=3,解得x=4,则B(4,3),
x+1=3,解得x=4,则B(4,3),
把A(﹣2,0),B(4,3)代入y=ax2+bx﹣3得 ![]() ,解得
,解得 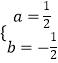 ,
,
∴抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x﹣3;
x﹣3;
②过B作BE⊥x轴于点E,如图1,
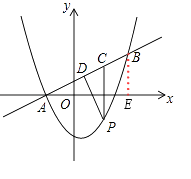
AE=4﹣(﹣2)=6,AB= ![]() =3
=3 ![]() ,
,
在Rt△ABE中,sin∠ABE= ![]() =
= ![]() =
= ![]() ,
,
∵PC∥BE,
∴sin∠ACP=sin∠ABE= ![]() ;
;
(2)
解:设P(m, ![]() m2﹣
m2﹣ ![]() m﹣3),则C(m,
m﹣3),则C(m, ![]() m+1),BM=4﹣m,
m+1),BM=4﹣m,
∴PC= ![]() m+1﹣(
m+1﹣( ![]() m2﹣
m2﹣ ![]() m﹣3)=﹣
m﹣3)=﹣ ![]() m2+m+4,
m2+m+4,
∵sin∠ACP= ![]() =
= ![]() ,
,
∴PD=﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() =﹣
=﹣ ![]() (m﹣1)2+
(m﹣1)2+ ![]() ,
,
当m=1时,线段PD长的最大值为 ![]() ;
;
②作BM⊥PC,交PC的延长线于点M,作DN⊥PC于点N,如图,
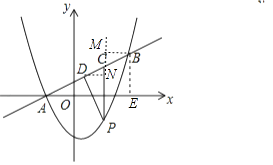
∵sinP=sin∠BAE= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴DN= ![]() (
( ![]() m2+
m2+ ![]() m+
m+ ![]() )=﹣
)=﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() ,
,
∵DN∥BM,
∴ ![]() =
= ![]() ,
,
∵线段PC把△PDB分成两个三角形的面积之比为9:10,
∴当 ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
整理得2m2﹣13m+20=0,解得m1= ![]() ,m2=4(舍去);
,m2=4(舍去);
当 ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
整理得9m2﹣68m+128=0,解得m1= ![]() ,m2=4(舍去);
,m2=4(舍去);
综上所述,m的值为 ![]() 或
或 ![]() ;
;
③存在.
如图2,连接PB交x轴于Q,
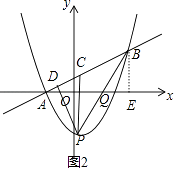
∵∠PDC=∠BDP,
∴当DPC=∠DBP时,△DPC∽△DBP,
而∠DPC=∠BAE,
∴∠BAE=∠ABP,
∴QA=QB,
设Q(t,0),则QA=QB=t+2,EQ=4﹣t,
在Rt△BQE中,(4﹣t)2+32=t2,解得t= ![]() ,则Q(
,则Q( ![]() ,0),
,0),
设直线BQ的解析式为y=px+q,
把B(4,3),Q( ![]() ,0)代入得
,0)代入得 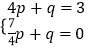 ,解得
,解得 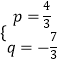 ,
,
∴直线BQ的解析式为y= ![]() x﹣
x﹣ ![]() ,
,
解方程组 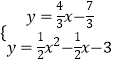 得
得 ![]() 或
或 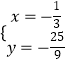 ,
,
∴P(﹣ ![]() ,﹣
,﹣ ![]() ),
),
∴m=﹣ ![]() .
.
【解析】(1)①由直线解析式可求得A、B两点的坐标,代入抛物线解析式可求得a、b的值,则可求得抛物线解析式;②过B作BE⊥x轴于点E,在Rt△ABE中可求得sin∠ABE,则可求得sin∠ACP;(2)①用m可表示出C点坐标,则可表示出PC的长,利用其正弦值可表示出PD的长,利用二次函数的性质可求得其最大值;②作BM⊥PC,交PC的延长线于点M,作DN⊥PC于点N,则可用m表示DN和BM,由面积的比得到DC与BC的比,然后利用相似比可得到m的方程,可求得m的值;③如图2,连接PB交x轴于Q,只有当DPC=∠DBP时,△DPC∽△DBP,于是可证明QA=QB,设Q(t,0),则QA=QB=t+2,EQ=4﹣t,利用勾股定理得到(4﹣t)2+32=t2 , 解得t= ![]() ,则Q(
,则Q( ![]() ,0),再利用待定系数法求出直线BQ的解析式为y=
,0),再利用待定系数法求出直线BQ的解析式为y= ![]() x﹣
x﹣ ![]() ,然后解方程组
,然后解方程组 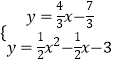 得P点坐标,从而得到m的值.
得P点坐标,从而得到m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上两点A、B所表示的数分别为a和b,且满足|a+3|+(b-9)2018=0,O为原点
(1) 试求a和b的值
(2) 点C从O点出发向右运动,经过3秒后点C到A点的距离是点C到B点距离的3倍,求点C的运动速度?
(3) 点D以1个单位每秒的速度从点O向右运动,同时点P从点A出发以5个单位每秒的速度向左运动,点Q从点B出发,以20个单位每秒的速度向右运动.在运动过程中,M、N分别为PD、OQ的中点,问
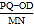 的值是否发生变化,请说明理由.
的值是否发生变化,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为2的正三角形中,将其内切圆和三个角切圆(与角两边及三角形内切圆都相切的圆)的内部挖去,则此三角形剩下部分(阴影部分)的面积为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个定点坐标分别为A(﹣1,3),B(﹣1,1),C(﹣3,2).

(1)请画出△ABC关于y轴对称的△A1B1C1;
(2)以原点O为位似中心,将△A1B1C1放大为原来的2倍,得到△A2B2C2 , 请在第三象限内画出△A2B2C2 , 并求出 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】小王乘公共汽车从甲地到相距40千米的乙地办事,然后乘出租车返回,出租车的平均速度比公共汽车多20千米/时,回来时路上所花时间比去时节省了
 ,设公共汽车的平均速度为x千米/时,则下面列出的方程中正确的是( )
,设公共汽车的平均速度为x千米/时,则下面列出的方程中正确的是( )
A.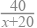 =
=  ×
× 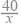
B.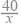 =
=  ×
× 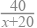
C.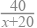 +
+  =
= 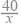
D.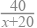 ﹣
﹣  =
= 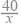
-
科目: 来源: 题型:
查看答案和解析>>【题目】某爱心企业在政府的支持下投入资金,准备修建一批室外简易的足球场和篮球场,供市民免费使用,修建1个足球场和1个篮球场共需8.5万元,修建2个足球场和4个篮球场共需27万元.
(1)求修建一个足球场和一个篮球场各需多少万元?
(2)该企业预计修建这样的足球场和篮球场共20个,投入资金不超过90万元,求至少可以修建多少个足球场?
-
科目: 来源: 题型:
查看答案和解析>>【题目】2013年6月,某中学结合广西中小学阅读素养评估活动,以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:

(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图(图1)补充完整;
(3)求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;
(4)如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.
相关试题

