【题目】如图,已知AB=10,P是线段AB上的任意一点,在AB的同侧分别以AP、PB为边作等边三角形APC和等边三角形PBD,连结CD.
(1)当AP=6时,求CD的长;
(2)当AP为多少时,CD的值最小,最小值是多少?

参考答案:
【答案】(1)2![]() ;(2)当AP=5时,CD的长度最小,最小值是5.
;(2)当AP=5时,CD的长度最小,最小值是5.
【解析】
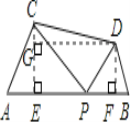
(1)如图,过C作CE⊥AB于E,过D作DF⊥PB于F,过D作DG⊥CE于G.即可得四边形DFEG为矩形.根据等边三角形的性质及矩形的性质求得EF=5,CG=![]() ,再利用勾股定理求得CD的长即可;(2)在(1)的基础上可得CD=
,再利用勾股定理求得CD的长即可;(2)在(1)的基础上可得CD=![]() ,当CG=0时,CD有最小值,由此求得CD的长即可.
,当CG=0时,CD有最小值,由此求得CD的长即可.
(1)如图,过C作CE⊥AB于E,过D作DF⊥PB于F,过D作DG⊥CE于G.即可得四边形DFEG为矩形.
∵AB=10,AP=6,
∴PB=4,
∵△APC和△PBD是等边三角形,CE⊥AB , DF⊥PB,
∴EP=![]() AP=3,PF=
AP=3,PF=![]() PB=2,
PB=2,
∴EF=EP+FP=5.
在Rt△DPF中,DP=4,PF=2,
由勾股定理求得DF=![]() .
.
在Rt△CEP中,PC=6,PE=3,
由勾股定理求得CE=![]() .
.
由矩形的性质可得,DG=EF=5,EG=DF,
∴CG=![]() .
.
在Rt△CGD中,DG=5,CG=![]() ,由勾股定理求得CD=2
,由勾股定理求得CD=2![]() ;
;
(2)如图, 由(1)得,DG=EF=![]() AB=5,CD≥DG,
AB=5,CD≥DG,

∴CD=![]() ,故CG=0时,CD有最小值,
,故CG=0时,CD有最小值,
当P为AB中点时,有CD=DG=5,
所以CD长度的最小值是5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市居民使用自来水按如下标准收费(水费按月缴纳):

(1)当a=2时,某用户一个月用了28 m3水,求该用户这个月应缴纳的水费;
(2)设某户月用水量为n 立方米,当n>20时,则该用户应缴纳的水费________元(用含a、n的整式表示);
(3)当a=2时,甲、乙两用户一个月共用水40m3 ,已知甲用户缴纳的水费超过了24元,设甲用户这个月用水xm3 ,试求甲、乙两用户一个月共缴纳的水费(用含x的整式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是( )
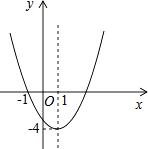
A.图象关于直线x=1对称
B.函数y=ax2+bx+c(a≠0)的最小值是﹣4
C.﹣1和3是方程ax2+bx+c=0(a≠0)的两个根
D.当x<1时,y随x的增大而增大 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:

(1)2018在第________行,第________列;
(2)由五个数组成的“
 ”中:
”中:① 这五个数的和可能是2019吗,为什么?
② 如果这五个数的和是60,直接写出这五个数;
(3)如果这五个数的和能否是2025,若能请求出这5个数;若不能请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
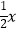 与双曲线y=
与双曲线y= 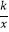 (k>0,x>0)交于点A,将直线y=
(k>0,x>0)交于点A,将直线y= 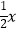 向上平移4个单位长度后,与y轴交于点C,与双曲线y=
向上平移4个单位长度后,与y轴交于点C,与双曲线y= 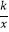 (k>0,x>0)交于点B,若OA=3BC,则k的值为( )
(k>0,x>0)交于点B,若OA=3BC,则k的值为( )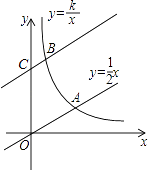
A.3
B.6
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】生活经验表明,靠墙摆放梯子时,若梯子底端离墙的距离约为梯子长度的
 ,则梯子比较稳定,如图,AB为一长度为6米的梯子.
,则梯子比较稳定,如图,AB为一长度为6米的梯子.(1)当梯子稳定摆放时,它的顶端能达到5.7米高的墙头吗?
(2)如图2,若梯子底端向左滑动(3
 ﹣2)米,那么梯子顶端将下滑多少米?
﹣2)米,那么梯子顶端将下滑多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上两点A、B所表示的数分别为a和b,且满足|a+3|+(b-9)2018=0,O为原点
(1) 试求a和b的值
(2) 点C从O点出发向右运动,经过3秒后点C到A点的距离是点C到B点距离的3倍,求点C的运动速度?
(3) 点D以1个单位每秒的速度从点O向右运动,同时点P从点A出发以5个单位每秒的速度向左运动,点Q从点B出发,以20个单位每秒的速度向右运动.在运动过程中,M、N分别为PD、OQ的中点,问
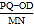 的值是否发生变化,请说明理由.
的值是否发生变化,请说明理由.
相关试题

