【题目】计算
(1)计算:﹣7+(20﹣3)
(2)化简:3a﹣2b+4c﹣2a﹣6c+b.
参考答案:
【答案】
(1)解:解:原式=﹣7+17=10
(2)解:解:原式=(3a﹣2a)+(﹣2b+b)+(4c﹣6c)=a﹣b﹣2c
【解析】(1)根据有理数的加减运算即可求出答案.(2)根据合并同类项的法则即可求出答案.
【考点精析】本题主要考查了有理数的加减混合运算的相关知识点,需要掌握混合运算法则:先乘方,后乘除,最后加减才能正确解答此题.
-
科目: 来源: 题型:
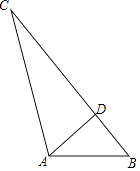
查看答案和解析>>【题目】综合题如图,D是BC上一点,若AB=10,AD=8,AC=17,BD=6,求BC的长.
(1)已知:x= +1,y=
+1,y=  ﹣1,求
﹣1,求  的值;
的值;
(2)如图,D是BC上一点,若AB=10,AD=8,AC=17,BD=6,求BC的长.
-
科目: 来源: 题型:
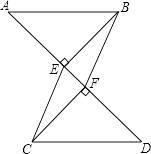
查看答案和解析>>【题目】如图,已知AB∥CD,BE⊥AD于点E,CF⊥AD于点F,且AF=DE,求证:四边形BECF是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蒜薹生产基地喜获丰收,收获蒜薹200吨.经市场调查,可采用批发、零售、冷库储藏后销售三种方式,并按这三种方式销售,计划平均每吨的售价及成本如下表:
销售方式
批发
零售
储藏后销售
售价(元/吨)
3000
4500
5500
成本(元/吨)
700
1000
1200
若经过一段时间,蒜薹按计划全部售出获得的总利润为y(元),蒜薹零售x(吨),且零售量是批发量的
 .
.
(1)求y与x之间的函数关系式;
(2)由于受条件限制,经冷库储藏售出的蒜薹最多80吨,求该生产基地按计划全部售完蒜薹获得的最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
把两个相同的数连接在一起就得到一个新数,我们把它称为“连接数”,例如:234234,3939…等,都是连接数,其中,234234称为六位连接数,3939称为四位连接数.
(1)请写出一个六位连接数 , 它(填“能”或“不能”)被13整除.
(2)是否任意六位连接数,都能被13整除,请说明理由.
(3)若一个四位连接数记为M,它的各位数字之和的3倍记为N,M﹣N的结果能被13整除,这样的四位连接数有几个? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图1在锐角△ABC中,∠ABC=45°,AD⊥BC于点D,BE⊥AC于点E,BE与AD交于点F.
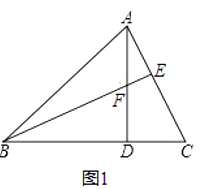
(1)若BF=5,DC=3,求AB的长;
(2)在图1上过点F作BE的垂线,过点A作AB的垂线,链条垂线交于点G,连接BG,得如图2.
①求证:∠BGF=45°;
②求证:AB=AG+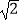 AF.
AF.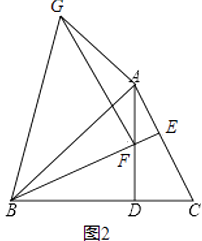
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),平面直角坐标系中,一次函数y=﹣x+1的图象与y轴交于点A,点B是第二象限一次函数y=﹣x+1的图象上一点,且S△OAB=3,点C的坐标为(﹣2,﹣3).
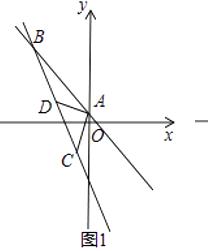
(1)求A,B的坐标;
(2)如图(1)若点D是线段BC上一点,且三角形ABD的面积是三角形ABC的一半,求△ABC的面积和点D的坐标;
(3)在(2)的条件下,如图(2),将线段AC沿直线AB平移,点A的对应点为A1 , 点C的对应点为C1 , 连接A1D,C1D,当△A1C1D直角三角形时,求A1的坐标.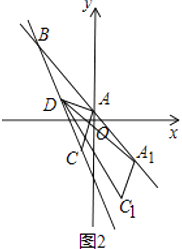
相关试题

