【题目】如图(1),平面直角坐标系中,一次函数y=﹣x+1的图象与y轴交于点A,点B是第二象限一次函数y=﹣x+1的图象上一点,且S△OAB=3,点C的坐标为(﹣2,﹣3).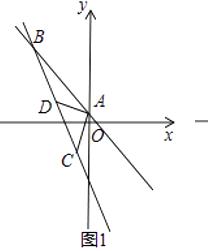
(1)求A,B的坐标;
(2)如图(1)若点D是线段BC上一点,且三角形ABD的面积是三角形ABC的一半,求△ABC的面积和点D的坐标;
(3)在(2)的条件下,如图(2),将线段AC沿直线AB平移,点A的对应点为A1 , 点C的对应点为C1 , 连接A1D,C1D,当△A1C1D直角三角形时,求A1的坐标.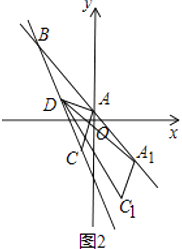
参考答案:
【答案】
(1)解:∵一次函数y=﹣x+1的图象与y轴交于点A,
∴当x=0时,y=1,
∴点A的坐标为(0,1),
∴OA=1
∵S△OAB=3,
∴ ![]() |xB|OA=3,
|xB|OA=3,
∴|xB|=6,
∵点B是第二象限一次函数y=﹣x+1的图象上一点,
∴B的横坐标为:﹣6,
则y=﹣(﹣6)+1=7,
∴点B的坐标为:(﹣6,7)
(2)解:如图1,过点B作BE⊥x轴,过点C作CF⊥y轴于点F,交BE于点E, 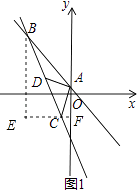
∵点C的坐标为(﹣2,﹣3),
∴BE=10,EF=6,EC=4,CF=2,AF=4,
∴S△ABC=S梯形ABEF﹣S△ACF﹣S△BEC= ![]() ×(4+10)×6﹣
×(4+10)×6﹣ ![]() ×4×2﹣
×4×2﹣ ![]() ×10×4=18;
×10×4=18;
∵点D是线段BC上一点,且三角形ABD的面积是三角形ABC的一半,
∴点D是BC的中点,
∴点D的坐标为:(﹣4,2)
(3)解:如图2,∵A(0,1),C(﹣2,﹣3),
∴由平移可知:点C是点A向左平移2个单位,再向下平移4个单位所得,
设A1(x,﹣x+1),则C1(x﹣2,﹣x+1﹣4),即(x﹣2,﹣x﹣3),
当△A1C1D直角三角形时,分三种情况:
①当∠DA1C1=90°时,如图2,由勾股定理得: ![]() =
= ![]() ,
,
∴(x+4)2+(﹣x+1﹣2)2+(x﹣2﹣x)2+(﹣x﹣3+x﹣1)2=(x﹣2+4)2+(﹣x﹣3﹣2)2
解得:x=2,
∴A1(2,﹣1);
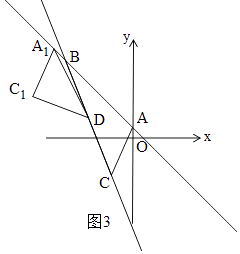
②当∠A1C1D=90°时,如图3,由勾股定理得: ![]() ,
, 
∴(x﹣2﹣x)2+(﹣x﹣3+x﹣1)2+(x﹣2+4)2+(﹣x﹣3﹣2)2=(x+4)2+(﹣x+1﹣2)2,
解得:x=﹣8,
∴A1(﹣8,9);
③当∠A1DC1=90°时,如图4和图5,由勾股定理得:A1D2+C1D2=A1C12,
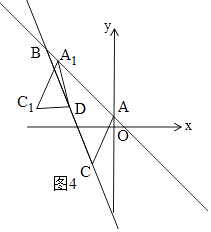
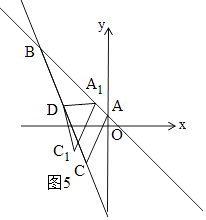
∴(x+4)2+(﹣x+1﹣2)2+(x﹣2+4)2+(﹣x﹣3﹣2)2=(x﹣2﹣x)2+(﹣x﹣3+x﹣1)2,
2x2+12x+13=0,
解得:x= ![]() ,
,
∴A1( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() );
);
综上所述,点A1的坐标为:(2,﹣1)或(﹣8,9)或( ![]() ,
, ![]()
![]() ,
, ![]() )
)
【解析】①一次函数y=﹣x+1的图象与y轴交于点A,求出点A的坐标为(0,1),点B是第二象限一次函数y=﹣x+1的图象上一点,得到B的横坐标为﹣6,求出点B的坐标为:(﹣6,7);②过点B作BE⊥x轴,过点C作CF⊥y轴于点F,交BE于点E,点C的坐标为(﹣2,﹣3),求出BE=10,EF=6,EC=4,CF=2,AF=4,S△ABC=S梯形ABEF﹣S△ACF﹣S△BEC=18,求出点D的坐标为:(﹣4,2);③由平移可知:点C是点A向左平移2个单位,再向下平移4个单位所得,当△A1C1D直角三角形时,分三种情况当∠DA1C1=90°时,如图2,由勾股定理得: A 1 D 2 + A 1 C 1 2 = D C 1 2 ,求出A1(2,﹣1);当∠A1C1D=90°时,由勾股定理得x=﹣8,得到A1(﹣8,9);当∠A1DC1=90°时,由勾股定理求出x的值,得到A1的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)计算:﹣7+(20﹣3)
(2)化简:3a﹣2b+4c﹣2a﹣6c+b. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
把两个相同的数连接在一起就得到一个新数,我们把它称为“连接数”,例如:234234,3939…等,都是连接数,其中,234234称为六位连接数,3939称为四位连接数.
(1)请写出一个六位连接数 , 它(填“能”或“不能”)被13整除.
(2)是否任意六位连接数,都能被13整除,请说明理由.
(3)若一个四位连接数记为M,它的各位数字之和的3倍记为N,M﹣N的结果能被13整除,这样的四位连接数有几个? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图1在锐角△ABC中,∠ABC=45°,AD⊥BC于点D,BE⊥AC于点E,BE与AD交于点F.
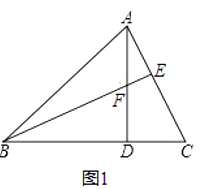
(1)若BF=5,DC=3,求AB的长;
(2)在图1上过点F作BE的垂线,过点A作AB的垂线,链条垂线交于点G,连接BG,得如图2.
①求证:∠BGF=45°;
②求证:AB=AG+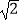 AF.
AF.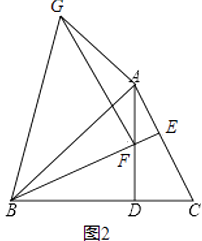
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数
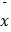 与方差s2:
与方差s2:甲
乙
丙
丁
平均数
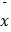 (cm)
(cm)561
560
561
560
方差s2(cm2)
3.5
3.5
15.5
16.5
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A.甲
B.乙
C.丙
D.丁 -
科目: 来源: 题型:
查看答案和解析>>【题目】天义地区某天的最高气温是8℃,最低气温是﹣2℃,则该地这一天的温差是( )
A.10℃
B.﹣6℃
C.6℃
D.﹣10℃ -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c是三角形的三边,那么代数式(a﹣b)2﹣c2的值( )
A. 大于零 B. 小于零 C. 等于零 D. 不能确定
相关试题

