【题目】如图,已知AB∥CD,BE⊥AD于点E,CF⊥AD于点F,且AF=DE,求证:四边形BECF是平行四边形.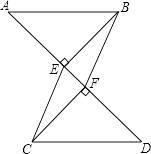
参考答案:
【答案】证明:∵BE⊥AD,CF⊥AD,
∴∠AEB=∠DFC=90°,
∵AB∥CD,
∴∠A=∠D,
∵AF=DE,
∴AE=DF,
在△AEB与△DFC中,
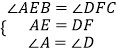 ,
,
∴△AEB≌△DFC(ASA),
∴BE=CF.
∵BE⊥AD,CF⊥AD,
∴BE∥CF.
∴四边形BECF是平行四边形.
【解析】由BE⊥AD,CF⊥AD,得到∠AEB=∠DFC=90°,由AB∥CD得到∠A=∠D,再由AF=DE得到AE=DF,得到△AEB≌△DFC(ASA),得出BE=CF,再由BE⊥AD,CF⊥AD,得到BE∥CF,由四边形的定义判定四边形BECF是平行四边形.
【考点精析】通过灵活运用平行四边形的判定,掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】红红和娜娜按如图所示的规则玩一次“锤子、剪刀、布”游戏,下列命题中错误的是( )

A.红红不是胜就是输,所以红红胜的概率为

B.红红胜或娜娜胜的概率相等
C.两人出相同手势的概率为
D.娜娜胜的概率和两人出相同手势的概率一样
-
科目: 来源: 题型:
查看答案和解析>>【题目】自习课时,同学抬头看见挂在黑板上方的时钟显示为9:30,此时时针与分针的夹角是度.
-
科目: 来源: 题型:
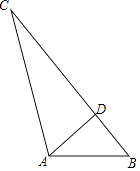
查看答案和解析>>【题目】综合题如图,D是BC上一点,若AB=10,AD=8,AC=17,BD=6,求BC的长.
(1)已知:x= +1,y=
+1,y=  ﹣1,求
﹣1,求  的值;
的值;
(2)如图,D是BC上一点,若AB=10,AD=8,AC=17,BD=6,求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蒜薹生产基地喜获丰收,收获蒜薹200吨.经市场调查,可采用批发、零售、冷库储藏后销售三种方式,并按这三种方式销售,计划平均每吨的售价及成本如下表:
销售方式
批发
零售
储藏后销售
售价(元/吨)
3000
4500
5500
成本(元/吨)
700
1000
1200
若经过一段时间,蒜薹按计划全部售出获得的总利润为y(元),蒜薹零售x(吨),且零售量是批发量的
 .
.
(1)求y与x之间的函数关系式;
(2)由于受条件限制,经冷库储藏售出的蒜薹最多80吨,求该生产基地按计划全部售完蒜薹获得的最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)计算:﹣7+(20﹣3)
(2)化简:3a﹣2b+4c﹣2a﹣6c+b. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
把两个相同的数连接在一起就得到一个新数,我们把它称为“连接数”,例如:234234,3939…等,都是连接数,其中,234234称为六位连接数,3939称为四位连接数.
(1)请写出一个六位连接数 , 它(填“能”或“不能”)被13整除.
(2)是否任意六位连接数,都能被13整除,请说明理由.
(3)若一个四位连接数记为M,它的各位数字之和的3倍记为N,M﹣N的结果能被13整除,这样的四位连接数有几个?
相关试题

