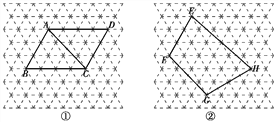
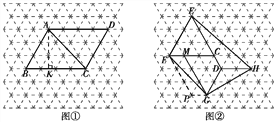
【题目】图中的虚线网格是等边三角形网格,它的每一个小三角形都是边长为1的等边三角形.
(1)边长为1的等边三角形的高=____;
(2)图①中的ABCD的对角线AC的长=____;
(3)图②中的四边形EFGH的面积=____.
参考答案:
【答案】 ![]()
![]() 8
8![]()
【解析】分析:(1)利用等边三角形的性质和勾股定理求出高;
(2)要求AC的长,构造直角三角形,应用勾股定理求出.
(3)要求四边形EFGH的面积,先将其分割,然后求每部分的面积,再相加和即可.
详解:(1)边长为1的等边三角形的高=![]() =
=![]() .
.
(2)过点A作AK⊥BC于K(如图①),
由图①知,ABCD的面积等于24个小等边三角形的面积和,由(1)知每个小等边三角形的面积为![]() ×1×
×1×![]() =
=![]() ,∴SABCD=24×
,∴SABCD=24×![]() =6
=6![]() .又SABCD=BC·AK,BC=4,∴AK=6
.又SABCD=BC·AK,BC=4,∴AK=6![]() ÷4=
÷4=![]() ,又在Rt△ABK中,AB=3,∴BK=
,又在Rt△ABK中,AB=3,∴BK=![]() =
=![]() ,∴KC=
,∴KC=![]() ,
,
∴AC=![]() =
=![]() .
.
(3)如图②所示,将四边形EFGH分割成五部分,以FG为对角线构造FPGM,
∵FPGM含有6个小等边三角形,
∴S△FGM=3S小等边三角形,
同理可得S△DGH=4S小等边三角形,S△EFC=9S小等边三角形,S△EDH=8S小等边三角形,又S四边形CMGD=8S小等边三角形,
由(2)知小等边三角形的面积为![]() ,
,
∴S四边形EFGH=(3+4+9+8+8)×![]() =8
=8![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为6
 的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,过点C作EG的垂线CH,垂足为点H,连接BH,BH=8.有下列结论:
的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,过点C作EG的垂线CH,垂足为点H,连接BH,BH=8.有下列结论:①∠CBH=45°;②点H是EG的中点;③EG=4
 ;④DG=2
;④DG=2 .
.其中,正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠D=∠BCD=90°,∠B=60°,AB=6,AD=9,点E是CD上的一个动点(E不与D重合),过点E作EF∥AC,交AD于点F(当E运动到C时,EF与AC重合),把△DEF沿着EF对折,点D的对应点是点G.设DE=x,△GEF与四边形ABCD重叠部分的面积为y.
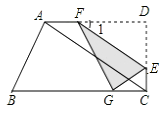
(1)求CD的长及∠1的度数;
(2)若点G恰好在BC上,求此时x的值;
(3)求y与x之间的函数关系式,并求x为何值时,y的值最大?最大值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】2016年为更好地宣传“开车不喝酒,喝酒不开车”的驾车理念,某市一家报社设计了如图的调查问卷(单选).在随机调查了某市全部10000名司机中的部分司机后,统计整理并制作了如下的统计图:

根据以上信息解答下列问题:
(1)补全条形统计图,并计算扇形统计图中m=;
(2)该市支持选项C的司机大约有多少人?
(3)若要从该市支持选项C的司机中随机选择200名,给他们签订“永不酒驾”的保证书,则支持该选项的司机小李被选中的概率是多少? -
科目: 来源: 题型:
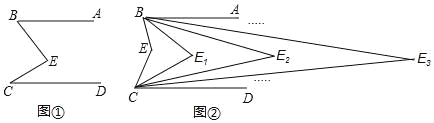
查看答案和解析>>【题目】如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En.
(1)如图①,求证:∠BEC=∠ABE+∠DCE;
(2)如图②,求证:∠BE2C=
 ∠BEC;
∠BEC;(3)猜想:若∠En=α度,那∠BEC等于多少度?(直接写出结论).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市篮球队到市一中选拔一名队员.教练对王亮和李刚两名同学进行5次3分球投篮测试,每人每次投10个球,图记录的是这两名同学5次投篮所投中的个数.

(1)请你根据图中的数据,填写下表;
姓名
平均数
众数
方差
王亮
7
李刚
7
2.8
(2)你认为谁的成绩比较稳定,为什么?
(3)若你是教练,你打算选谁?简要说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知函数y=-
 x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点E,点E的横坐标为3.
x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点E,点E的横坐标为3.(1)求点A的坐标;
(2)在x轴上有一点F(a,0),过点F作x轴的垂线,分别交函数y=-
 x+b和y=x的图象于点C、D,若以点B、O、C、D为顶点的四边形为平行四边形,求a的值.
x+b和y=x的图象于点C、D,若以点B、O、C、D为顶点的四边形为平行四边形,求a的值.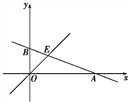
相关试题

