【题目】2016年为更好地宣传“开车不喝酒,喝酒不开车”的驾车理念,某市一家报社设计了如图的调查问卷(单选).在随机调查了某市全部10000名司机中的部分司机后,统计整理并制作了如下的统计图: 
根据以上信息解答下列问题:
(1)补全条形统计图,并计算扇形统计图中m=;
(2)该市支持选项C的司机大约有多少人?
(3)若要从该市支持选项C的司机中随机选择200名,给他们签订“永不酒驾”的保证书,则支持该选项的司机小李被选中的概率是多少?
参考答案:
【答案】
(1)20
(2)解:支持选项C的人数大约为:90÷300=30%,10000×30%=3000(人).
答:该市支持选项C的司机大约有3000人
(3)解:∵该市支持选项C的司机总人数=10000×30%=3000人,
∴小李被选中的概率是 ![]() ,
,
答:支持该选项的司机小李被选中的概率是 ![]()
【解析】解:(1)∵69÷23%﹣60﹣69﹣36﹣45=90(人).
∴C选项的频数为90,
补全图形如下: .
.
∵m%=60÷(69÷23%)=20%.
∴m=20,
所以答案是:20;
【考点精析】认真审题,首先需要了解扇形统计图(能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况),还要掌握条形统计图(能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个不同的一次函数y=ax+b与y=bx+a的图象在同一平面直角坐标系内的位置可能是( )
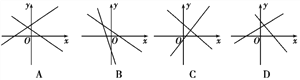
A. A B. B C. C D. D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为6
 的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,过点C作EG的垂线CH,垂足为点H,连接BH,BH=8.有下列结论:
的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,过点C作EG的垂线CH,垂足为点H,连接BH,BH=8.有下列结论:①∠CBH=45°;②点H是EG的中点;③EG=4
 ;④DG=2
;④DG=2 .
.其中,正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠D=∠BCD=90°,∠B=60°,AB=6,AD=9,点E是CD上的一个动点(E不与D重合),过点E作EF∥AC,交AD于点F(当E运动到C时,EF与AC重合),把△DEF沿着EF对折,点D的对应点是点G.设DE=x,△GEF与四边形ABCD重叠部分的面积为y.
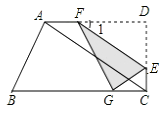
(1)求CD的长及∠1的度数;
(2)若点G恰好在BC上,求此时x的值;
(3)求y与x之间的函数关系式,并求x为何值时,y的值最大?最大值是多少? -
科目: 来源: 题型:
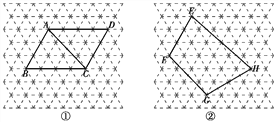
查看答案和解析>>【题目】图中的虚线网格是等边三角形网格,它的每一个小三角形都是边长为1的等边三角形.
(1)边长为1的等边三角形的高=____;
(2)图①中的ABCD的对角线AC的长=____;
(3)图②中的四边形EFGH的面积=____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,
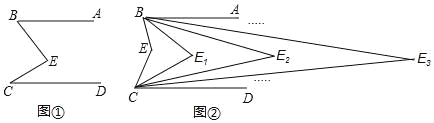
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En.
(1)如图①,求证:∠BEC=∠ABE+∠DCE;
(2)如图②,求证:∠BE2C=
 ∠BEC;
∠BEC;(3)猜想:若∠En=α度,那∠BEC等于多少度?(直接写出结论).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市篮球队到市一中选拔一名队员.教练对王亮和李刚两名同学进行5次3分球投篮测试,每人每次投10个球,图记录的是这两名同学5次投篮所投中的个数.

(1)请你根据图中的数据,填写下表;
姓名
平均数
众数
方差
王亮
7
李刚
7
2.8
(2)你认为谁的成绩比较稳定,为什么?
(3)若你是教练,你打算选谁?简要说明理由.
相关试题

