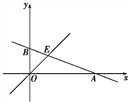
【题目】如图,已知函数y=-![]() x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点E,点E的横坐标为3.
x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点E,点E的横坐标为3.
(1)求点A的坐标;
(2)在x轴上有一点F(a,0),过点F作x轴的垂线,分别交函数y=-![]() x+b和y=x的图象于点C、D,若以点B、O、C、D为顶点的四边形为平行四边形,求a的值.
x+b和y=x的图象于点C、D,若以点B、O、C、D为顶点的四边形为平行四边形,求a的值.
参考答案:
【答案】(1)A点的坐标为(12,0);(2)a=6
【解析】分析:(1)根据函数的解析式求出E点的坐标,然后根据待定系数法求出b的值,然后求出与x轴的坐标即可;
(2)根据F点的坐标和垂直的意义,得到C、D点的横坐标均为a,然后根据两点的距离和平行四边形的性质得CD=OB,列方程求解即可.
详解:(1)把x=3代入y=x,得y=3,即E(3,3),
把点E的坐标代入y=-![]() x+b中,得b=4,
x+b中,得b=4,
故函数解析式为y=-![]() x+4,
x+4,
令y=0,得0=-![]() x+4,解得x=12,
x+4,解得x=12,
故A点的坐标为(12,0).
(2)直线AB的解析式为y=-![]() x+4,
x+4,
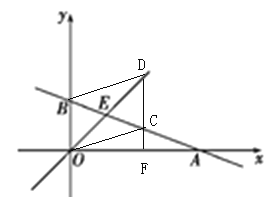
由题意可知,点C、D的横坐标均为a,
∴C![]() ,D(a,a),
,D(a,a),
∴CD=![]() =
=![]() ,
,
∵以点B、O、C、D为顶点的四边形为平行四边形,
∴CD=OB=4,即![]() =4,
=4,
解得a=6或a=0.经验证,当a=0时,直线CD与OB重合,不合题意,当a=6时符合题意.故a=6.
-
科目: 来源: 题型:
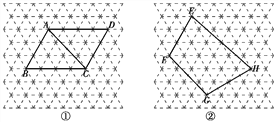
查看答案和解析>>【题目】图中的虚线网格是等边三角形网格,它的每一个小三角形都是边长为1的等边三角形.
(1)边长为1的等边三角形的高=____;
(2)图①中的ABCD的对角线AC的长=____;
(3)图②中的四边形EFGH的面积=____.
-
科目: 来源: 题型:
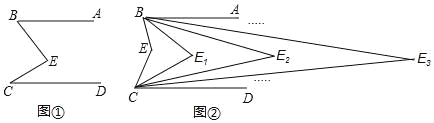
查看答案和解析>>【题目】如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En.
(1)如图①,求证:∠BEC=∠ABE+∠DCE;
(2)如图②,求证:∠BE2C=
 ∠BEC;
∠BEC;(3)猜想:若∠En=α度,那∠BEC等于多少度?(直接写出结论).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市篮球队到市一中选拔一名队员.教练对王亮和李刚两名同学进行5次3分球投篮测试,每人每次投10个球,图记录的是这两名同学5次投篮所投中的个数.

(1)请你根据图中的数据,填写下表;
姓名
平均数
众数
方差
王亮
7
李刚
7
2.8
(2)你认为谁的成绩比较稳定,为什么?
(3)若你是教练,你打算选谁?简要说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AE于点E.

(1)求证:△BEF∽△DBC.;
(2)若⊙O的半径为3,∠C=32°,求BE的长.(精确到0.01) -
科目: 来源: 题型:
查看答案和解析>>【题目】2016年春季,建阳区某服装商店分两次从批发市场购进同一款服装,数量之比是2:3,且第一、二次进货价分别为每件50元、40元,总共付了4400元的货款.
(1)求第一、二次购进服装的数量分别是多少件?
(2)由于该款服装刚推出时,很受欢迎,按每件70元销售了x件;后来,由于该服装滞销,为了及时处理库存,缓解资金压力,其剩余部分的按每件30元全部售完.当x的值至少为多少时,该服装商店才不会亏本. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于点F,连接AD、CF.
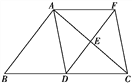
(1)求证:四边形ADCF是平行四边形;
(2)当△ABC满足什么条件时,四边形ADCF是菱形?为什么?
相关试题

