【题目】某市篮球队到市一中选拔一名队员.教练对王亮和李刚两名同学进行5次3分球投篮测试,每人每次投10个球,图记录的是这两名同学5次投篮所投中的个数.

(1)请你根据图中的数据,填写下表;
姓名 | 平均数 | 众数 | 方差 |
王亮 | 7 | ||
李刚 | 7 | 2.8 |
(2)你认为谁的成绩比较稳定,为什么?
(3)若你是教练,你打算选谁?简要说明理由.
参考答案:
【答案】(1)见解析;(2)王亮的成绩较稳定,理由见解析;(3)选王亮.理由见解析
【解析】分析:(1)根据平均数的定义,计算5次投篮成绩之和与5的商即为王亮每次投篮平均数;根据众数定义,王亮投篮出现次数最多的成绩即为其众数;
(2)先算出王亮的成绩的平均数,再根据方差公式计算王亮的投篮次数的方差.
(3)从平均数、众数、方差等不同角度分析,可得不同结果,关键是看参赛的需要.
详解:(1)王亮5次投篮,有3次投中7个,故7为众数;
方差s2=![]() [(6-7)2+(7-7)2+…+(7-7)2]=0.4.
[(6-7)2+(7-7)2+…+(7-7)2]=0.4.
李刚投篮投中个数的平均数为(4+7+7+8+9)÷5=7.填表如下:
姓名 | 平均数 | 众数 | 方差 |
王亮 | 7 | 7 | 0.4 |
李刚 | 7 | 7 | 2.8 |
(2)两人投篮投中个数的平均数、众数相同,从方差上看,王亮投篮成绩的方差小于李刚投篮成绩的方差.
故王亮的成绩较稳定.
(3)选王亮.理由:由(2)知王亮的投篮成绩较稳定,故选王亮.
(或选李刚.理由:由题图知李刚投中8个及以上球的次数较多,且每次测试,投中球个数呈上升趋势,投中率较高,故选李刚.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年为更好地宣传“开车不喝酒,喝酒不开车”的驾车理念,某市一家报社设计了如图的调查问卷(单选).在随机调查了某市全部10000名司机中的部分司机后,统计整理并制作了如下的统计图:

根据以上信息解答下列问题:
(1)补全条形统计图,并计算扇形统计图中m=;
(2)该市支持选项C的司机大约有多少人?
(3)若要从该市支持选项C的司机中随机选择200名,给他们签订“永不酒驾”的保证书,则支持该选项的司机小李被选中的概率是多少? -
科目: 来源: 题型:
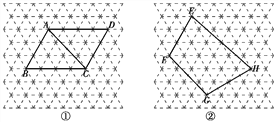
查看答案和解析>>【题目】图中的虚线网格是等边三角形网格,它的每一个小三角形都是边长为1的等边三角形.
(1)边长为1的等边三角形的高=____;
(2)图①中的ABCD的对角线AC的长=____;
(3)图②中的四边形EFGH的面积=____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,
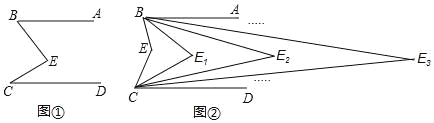
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En.
(1)如图①,求证:∠BEC=∠ABE+∠DCE;
(2)如图②,求证:∠BE2C=
 ∠BEC;
∠BEC;(3)猜想:若∠En=α度,那∠BEC等于多少度?(直接写出结论).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知函数y=-
 x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点E,点E的横坐标为3.
x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点E,点E的横坐标为3.(1)求点A的坐标;
(2)在x轴上有一点F(a,0),过点F作x轴的垂线,分别交函数y=-
 x+b和y=x的图象于点C、D,若以点B、O、C、D为顶点的四边形为平行四边形,求a的值.
x+b和y=x的图象于点C、D,若以点B、O、C、D为顶点的四边形为平行四边形,求a的值.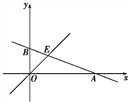
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AE于点E.

(1)求证:△BEF∽△DBC.;
(2)若⊙O的半径为3,∠C=32°,求BE的长.(精确到0.01) -
科目: 来源: 题型:
查看答案和解析>>【题目】2016年春季,建阳区某服装商店分两次从批发市场购进同一款服装,数量之比是2:3,且第一、二次进货价分别为每件50元、40元,总共付了4400元的货款.
(1)求第一、二次购进服装的数量分别是多少件?
(2)由于该款服装刚推出时,很受欢迎,按每件70元销售了x件;后来,由于该服装滞销,为了及时处理库存,缓解资金压力,其剩余部分的按每件30元全部售完.当x的值至少为多少时,该服装商店才不会亏本.
相关试题

