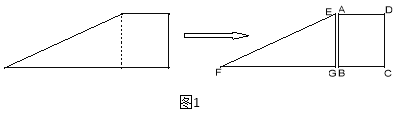
【题目】如图1,小红将一张直角梯形纸片沿虚线剪开,得到矩形和三角形两张纸片,测得AB=15,AD=12.在进行如下操作时遇到了下面的几个问题,请你帮助解决.
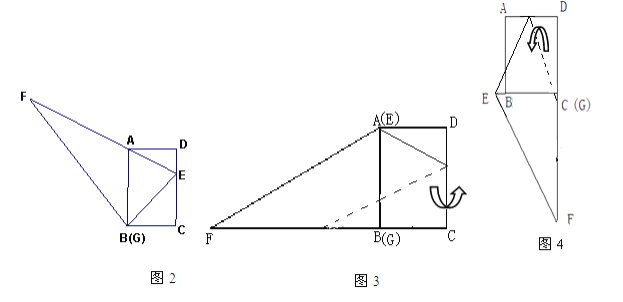
(1)将△EFG的顶点G移到矩形的顶点B处,再将三角形绕点B顺时针旋转使E点落在CD边上,此时,EF恰好经过点A(如图2)求FB的长度
(2)在(1)的条件下,小红想用△EFG包裹矩形ABCD,她想了两种包裹的方法如图3、图4,请问哪种包裹纸片的方法使得未包裹住的面积大?(纸片厚度忽略不计)请你通过计算说服小红。
参考答案:
【答案】(1)30;(2) 二种包裹纸片的方法使得未包裹住的面积相等.
【解析】
试题分析:(1)利用矩形的性质以及得出△ADE∽△FBE,求出即可;
(2)根据Rt△F,HN~Rt△F,EG,得到HN=3,从而S△AMH=144;由Rt△GBE~Rt△C,B,G,得到GB,=24,从而S△B,C,G=144,进行比较即可.
⑴BE=AD=15,在RtBCE中,CE2=B E2-BC2=152-122,求得CE=9,DE=6,
证Rt△ADE~Rt△FBE,
求得BF=30
⑵①如图1,将矩形ABCD和Rt△FBE以CD为轴翻折,则△AMH即为未包裹住的面积,

由Rt△F,HN~Rt△F,EG,得到HN=3,
从而S△AMH=144
②如图2,将矩形ABCD和Rt△ECF以AD为轴翻折,由Rt△GBE~Rt△C,B,G,得到GB,=24,

从而S△B,C,G=144,∴未包裹的面积为144.
∴按照二种包裹的方法未包裹的面积相等。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中以点A为圆心,AB为半径作圆A交网格于点C(如图(1)),过点C作圆的切线交网格于点D,以点A为圆心,AD为半径作圆交网格于点E(如图(2)).
问题:
(1)求∠ABC的度数;
(2)求证:△AEB≌△ADC;
(3)△AEB可以看作是由△ADC经过怎样的变换得到的?并判断△AED的形状(不用说明理由).
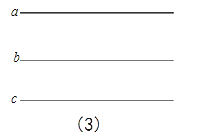
(4)如图(3),已知直线a,b,c,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形A′B′C′使三个顶点A′,B′,C′,分别在直线a,b,c上.要求写出简要的画图过程,不需要说明理由.
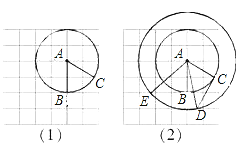
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)2+(﹣3)+(﹣6)+8
(2)1﹣(﹣4)÷22×
(3)( ﹣
﹣  +
+  )÷(﹣
)÷(﹣  )
)
(4)﹣12×8﹣8×( )3+4÷
)3+4÷  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣4x+m﹣1=0有两个相等的实数根,求m的值及方程的根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】判断正误.
(1)直径是圆的对称轴;
(2)平分弦的直径垂直于弦.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,分别过B,C向过点A的直线作垂线,垂足分别为点E,F.
(1)如图(1),过A的直线与斜边BC不相交时,求证:①△ABE≌△CAF; ②EF=BE+CF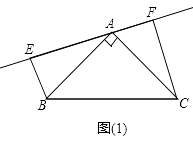
(2)如图(2),过A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,试求EF的长.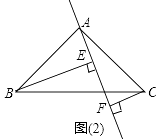
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店代销一批季节性服装,每套代销成本40元,第一个月每套销售定价为52元时,可售出180套;应市场变化调整第一个月的销售价,预计销售定价每增加1元,销售量将减少10套.若商店预计要在这两个月的代销中获利4160元,则第二个月销售定价每套_______元.
相关试题

