【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,分别过B,C向过点A的直线作垂线,垂足分别为点E,F.
(1)如图(1),过A的直线与斜边BC不相交时,求证:①△ABE≌△CAF; ②EF=BE+CF 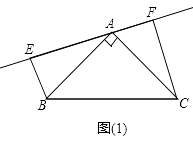
(2)如图(2),过A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,试求EF的长. 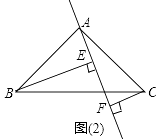
参考答案:
【答案】
(1)证明:
①∵BE⊥EF,CF⊥EF,
∴∠AEB=∠CFA=90°,
∴∠EAB+∠EBA=90°,
∵∠BAC=90°,
∴∠EAB+∠FAC=90°,
∴∠EBA=∠FAC,
在△AEB与△CFA中

∴△ABE≌△CAF(AAS),
②∵△ABE≌△CAF,
∴EA=FC,EB=FA,
∴EF=AF+AE
=BE+CF
(2)解:∵BE⊥AF,CF⊥AF
∴∠AEB=∠CFA=90°
∴∠EAB+∠EBA=90°
∵∠BAC=90°
∴∠EAB+∠FAC=90°
∴∠EBA=∠FAC,
在△AEB与△CFA中

∴△ABE≌△CAF(AAS),
∴EA=FC,EB=FA,
∴EF=FA﹣EA=EB﹣FC=10﹣3=7
【解析】(1)①由条件可求得∠EBA=FAC,利用AAS可证明△ABE≌△CAF;②利用全等三角形的性质可得EA=FC,EB=FA,利用线段的和差可证得结论;(2)同(1)可证明△ABE≌△CAF,可证得EF=FA﹣EA,代入可求得EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣4x+m﹣1=0有两个相等的实数根,求m的值及方程的根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,小红将一张直角梯形纸片沿虚线剪开,得到矩形和三角形两张纸片,测得AB=15,AD=12.在进行如下操作时遇到了下面的几个问题,请你帮助解决.
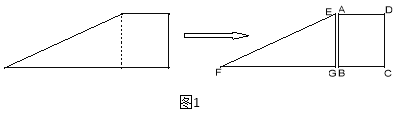
(1)将△EFG的顶点G移到矩形的顶点B处,再将三角形绕点B顺时针旋转使E点落在CD边上,此时,EF恰好经过点A(如图2)求FB的长度
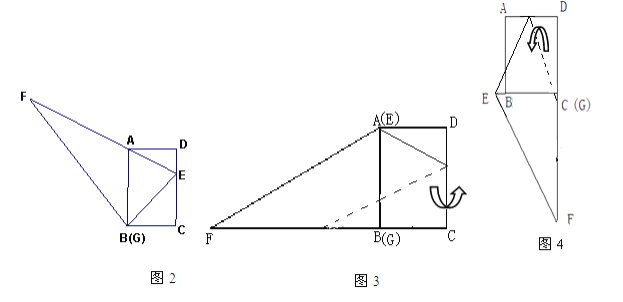
(2)在(1)的条件下,小红想用△EFG包裹矩形ABCD,她想了两种包裹的方法如图3、图4,请问哪种包裹纸片的方法使得未包裹住的面积大?(纸片厚度忽略不计)请你通过计算说服小红。
-
科目: 来源: 题型:
查看答案和解析>>【题目】判断正误.
(1)直径是圆的对称轴;
(2)平分弦的直径垂直于弦.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店代销一批季节性服装,每套代销成本40元,第一个月每套销售定价为52元时,可售出180套;应市场变化调整第一个月的销售价,预计销售定价每增加1元,销售量将减少10套.若商店预计要在这两个月的代销中获利4160元,则第二个月销售定价每套_______元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果|a|=|b|,那么a,b两个实数一定是( )
A.都等于0
B.一正一负
C.相等
D.相等或互为相反数 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ACE是以□ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若E点的坐标是(7,-3
 ),则D点的坐标是 ( )
),则D点的坐标是 ( )
A.(4,0)
B.( ,0)
,0)
C.(5,0)
D.( ,0)
,0)
相关试题

