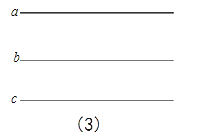
【题目】在正方形网格中以点A为圆心,AB为半径作圆A交网格于点C(如图(1)),过点C作圆的切线交网格于点D,以点A为圆心,AD为半径作圆交网格于点E(如图(2)).
问题:
(1)求∠ABC的度数;
(2)求证:△AEB≌△ADC;
(3)△AEB可以看作是由△ADC经过怎样的变换得到的?并判断△AED的形状(不用说明理由).
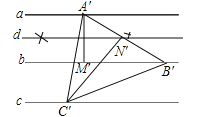
(4)如图(3),已知直线a,b,c,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形A′B′C′使三个顶点A′,B′,C′,分别在直线a,b,c上.要求写出简要的画图过程,不需要说明理由.
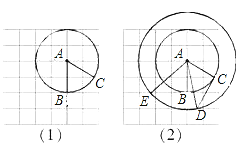
参考答案:
【答案】(1)∠ABC=60°;
(2)证明见解析;
(3)△AEB可以看作是由△ADC绕点A顺时针旋转60°得到的,△AED是等边三角形;
(4)作图及画图过程见解析.
【解析】试题分析:
(1)连接BC,通过证明△ABC是等边三角形,即可求出∠ABC的度数;
(2)在Rt△AEB与Rt△ADC中,通过HL证明△AEB≌△ADC;
(3)由旋转的性质即可得出△AED是等边三角形;
(4)利用HL定理可证△A′N′C′≌△A′M′B′,得∠C′A′N′=∠B′A′M′,于是∠B′A′C′=∠M′A′N′=60°,由A′B′=A′C′得△A′B′C′为等边三角形.
试题解析:
(1)连接BC,如图所示:
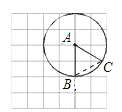
由网格可知点C在AB的中垂线上,
∴AC=BC,
∵AB=AC,∴AB=BC=AC,即△ABC是等边三角形.
∴∠ABC=60°;
(2)如图所示:
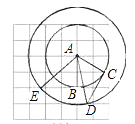
∵CD切⊙A于点C,
∴∠ACD=90°∠ABE=∠ACD=90°,
在Rt△AEB与Rt△ADC中,
∵AB=AC,AE=AD.
∴Rt△AEB≌Rt△ADC(HL);
(3)△AEB可以看作是由△ADC绕点A顺时针旋转60°得到的.△AED是等边三角形;
(4)①在直线a上任取一点,记为点A′,作A′M′⊥b,垂足为点M′;②作线段A′M′的垂直平分线,此直线记为直线d;③以点A′为圆心,A′M′长为半径画圆,与直线d交于点N′;④过点N′作N′C′⊥A′N′交直线c于点C′,连接A′C′;⑤以点A′为圆心,A′C′长为半径画圆,此圆交直线b于点B′;⑥连接A′B′、B′C′,则△A′B′C′为所求等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣3,0),C(2,0),将△ABC绕点B顺时针旋转一定角度后使A落在y轴上,与此同时顶点C恰好落在y=
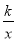 的图象上,则k的值为__.
的图象上,则k的值为__.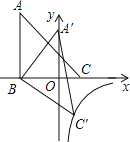
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)3a2b3÷ a3b
a3b  ab3
ab3
(2)(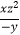 )3(
)3( 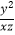 )4÷(
)4÷( 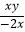 )3 .
)3 . -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的情境对话,然后解答问题

(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt
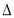 ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt
ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt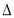 ABC是奇异三角形,求a:b:c;
ABC是奇异三角形,求a:b:c;(3)如图,AB是⊙O的直径,C是上一点(不与点A、B重合),D是半圆的中点,CD在直径AB的两侧,若在⊙O内存在点E使得AE=AD,CB=CE.
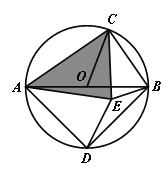
求证:
 ACE是奇异三角形;
ACE是奇异三角形;当
 ACE是直角三角形时,求∠AOC的度数.
ACE是直角三角形时,求∠AOC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)2+(﹣3)+(﹣6)+8
(2)1﹣(﹣4)÷22×
(3)( ﹣
﹣  +
+  )÷(﹣
)÷(﹣  )
)
(4)﹣12×8﹣8×( )3+4÷
)3+4÷  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣4x+m﹣1=0有两个相等的实数根,求m的值及方程的根.
-
科目: 来源: 题型:
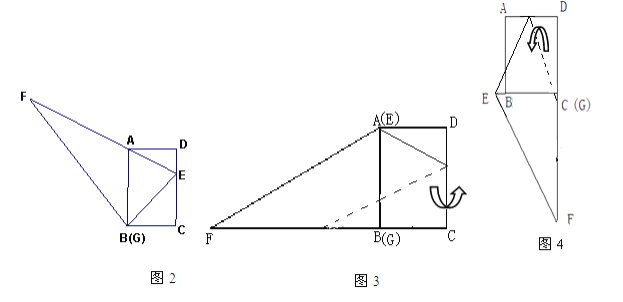
查看答案和解析>>【题目】如图1,小红将一张直角梯形纸片沿虚线剪开,得到矩形和三角形两张纸片,测得AB=15,AD=12.在进行如下操作时遇到了下面的几个问题,请你帮助解决.
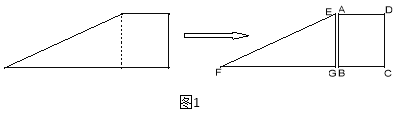
(1)将△EFG的顶点G移到矩形的顶点B处,再将三角形绕点B顺时针旋转使E点落在CD边上,此时,EF恰好经过点A(如图2)求FB的长度
(2)在(1)的条件下,小红想用△EFG包裹矩形ABCD,她想了两种包裹的方法如图3、图4,请问哪种包裹纸片的方法使得未包裹住的面积大?(纸片厚度忽略不计)请你通过计算说服小红。
相关试题

