【题目】如图所示,平面直角坐标系中,抛物线![]() 经过
经过![]() 、
、![]() 、
、![]() .过点
.过点![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() .点
.点![]() 是四边形
是四边形![]() 的对角线的交点,点
的对角线的交点,点![]() 在
在![]() 轴负半轴上,且
轴负半轴上,且![]() .
.
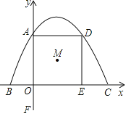
(1)求抛物线的解析式,并直接写出四边形![]() 的形状;
的形状;
(2)当点![]() 、
、![]() 从
从![]() 、
、![]() 两点同时出发,均以每秒
两点同时出发,均以每秒![]() 个长度单位的速度沿
个长度单位的速度沿![]() 、
、![]() 方向运动,点
方向运动,点![]() 运动到
运动到![]() 时
时![]() 、
、![]() 两点同时停止运动.设运动的时间为
两点同时停止运动.设运动的时间为![]() 秒,在运动过程中,以
秒,在运动过程中,以![]() 、
、![]() 、
、![]() 、
、![]() 四点为顶点的四边形的面积为
四点为顶点的四边形的面积为![]() ,求出
,求出![]() 与
与![]() 之间的函数关系式,并写出自变量的取值范围;
之间的函数关系式,并写出自变量的取值范围;
(3)在抛物线上是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是梯形?若存在,直接写出点
为顶点的四边形是梯形?若存在,直接写出点![]() 的坐标;不存在,说明理由.
的坐标;不存在,说明理由.
参考答案:
【答案】(1)![]() ,四边形
,四边形![]() 为正方形;(2)当
为正方形;(2)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;(3)在抛物线上存在点
;(3)在抛物线上存在点![]() ,
,![]() ,
,![]() ,
,![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是梯形.
为顶点的四边形是梯形.
【解析】
(1)由抛物线y=ax2+bx+c经过A(0,4)、B(-2,0)、C(6,0)三点,把三点坐标代入抛物线表达式中,联立方程解出a、b、c;
(2)过M作MN⊥OE于N,则MN=2,由题意可知CP=FQ=t,当0≤t<2时,OP=6-t,OQ=2-t,列出S与t的关系式,当t=2时,Q与O重合,点M、O、P、Q不能构成四边形,当2<t<6时,连接MO,ME则MO=ME且∠QOM=∠PEM=45°,可证三角形全等,进而计算出三角形面积;
(3)若B、C、F、N为顶点的四边形是梯形,则四边形有两边平行,设出N点的坐标,分类讨论两边平行时N点坐标满足的条件,进而求出N点坐标.
解:(1)∵抛物线经过![]() 、
、![]() 、
、![]() ,
,
∴![]() ,
,
![]() ,
,
解得![]() ,
,![]() ,
,![]() .
.
∴抛物线的解析式为![]() .
.
四边形![]() 为正方形.
为正方形.
(2)连接![]() .
.
根据题意,可知![]() ,
,![]() ,
,
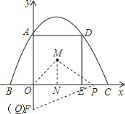
∴![]() ,
,
∴![]() ,
,
∵运动的时间为![]() ,
,
∴![]() ,
,
过![]() 作
作![]() 于
于![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
当![]() 时,
时,![]() 与
与![]() 重合,点
重合,点![]() 、
、![]() 、
、![]() 、
、![]() 不能构成四边形,
不能构成四边形,
当![]() 时,连接
时,连接![]() ,
,![]() 则
则![]() 且
且![]() ,
,
∵![]() ,
,![]() ,
,
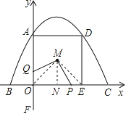
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 的面积
的面积![]() ,
,
综上所述,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(3)分三种情况:
①以![]() 为底边时,经过点
为底边时,经过点![]() 作
作![]() 的平行线,与抛物线交于点
的平行线,与抛物线交于点![]() 的坐标为
的坐标为![]() ;
;
②以![]() 为底边时,经过点
为底边时,经过点![]() 作
作![]() 的平行线,与抛物线交于点
的平行线,与抛物线交于点![]() 的坐标为
的坐标为![]() ;
;
③以![]() 为底边时,经过点
为底边时,经过点![]() 作
作![]() 的平行线,与抛物线交于点
的平行线,与抛物线交于点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
故在抛物线上存在点![]() ,
,![]() ,
,![]() ,
,![]() ,
,
使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是梯形.
为顶点的四边形是梯形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某星期天,八(1)班开展社会实践活动,第一小组花90元从蔬菜批发市场批发了黄瓜和茄子共40kg,到蔬菜市场去卖,黄瓜和茄子当天的批发价与零售价如表所示:
品名
黄瓜
茄子
批发价/(元/kg)
2.4
2
零售价/(元/kg)
3.6
2.8
(1)黄瓜和茄子各批发了多少kg?
(2)该小组当天卖完这些黄瓜和茄子可赚多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某食品零售店为食品厂代销一种面包,未售出的面包可以退回厂家.经统计销售情况发现,当这种面包的销售单价为7角时,每天卖出160个.在此基础上.单价每提高1角时,该零售店每天就会少卖出20个面包.设这种面包的销售单价为x角(每个面包的成本是5角).零售店每天销售这种面包的利润为y角.
(1)用含x的代数式分别表示出每个面包的利润与卖出的面包个数;
(2)求x与y之间的函数关系式:
(3)当这种面包的销售单价定为多少时,该零售店每天销售这种面包获得的利润最大?最大利润为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=45°,CD⊥AB,垂足为点D,M为线段DB上一动点(不包括端点),点N在直线AC左上方且∠NCM=135°,CN=CM,如图①.
(1)求证:∠ACN=∠AMC;
(2)记△ANC得面积为5,记△ABC得面积为5.求证:
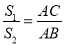 ;
;(3)延长线段AB到点P,使BP=BM,如图②.探究线段AC与线段DB满足什么数量关系时对于满足条件的任意点M,AN=CP始终成立?(写出探究过程)
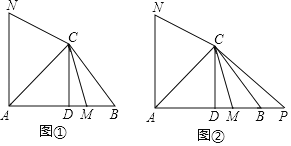
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示经过原点,给出以下四个结论:①abc=0,②a+b+c>0,③2a>b,④4ac﹣b2<0;其中正确的结论有( )
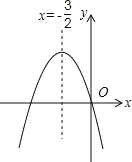
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一次函数y
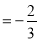 x+4的图象与x轴和y轴分别交于A、B两点.动点P从点A出发,在线段AO上以每秒1个单位长度的速度向点O作匀速运动,到达点O即停止运动.其中A、Q两点关于点P对称,以线段PQ为边向上作正方形PQMN.设运动时间为秒.如图①.
x+4的图象与x轴和y轴分别交于A、B两点.动点P从点A出发,在线段AO上以每秒1个单位长度的速度向点O作匀速运动,到达点O即停止运动.其中A、Q两点关于点P对称,以线段PQ为边向上作正方形PQMN.设运动时间为秒.如图①.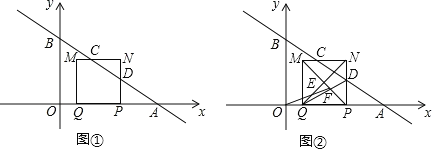
(1)当t=2秒时,OQ的长度为 ;
(2)设MN、PN分别与直线y
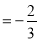 x+4交于点C、D,求证:MC=NC;
x+4交于点C、D,求证:MC=NC;(3)在运动过程中,设正方形PQMN的对角线交于点E,MP与QD交于点F,如图2,求OF+EN的最小值.
-
科目: 来源: 题型:
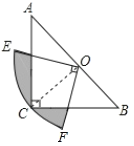
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为________.
相关试题

