【题目】某星期天,八(1)班开展社会实践活动,第一小组花90元从蔬菜批发市场批发了黄瓜和茄子共40kg,到蔬菜市场去卖,黄瓜和茄子当天的批发价与零售价如表所示:
品名 | 黄瓜 | 茄子 |
批发价/(元/kg) | 2.4 | 2 |
零售价/(元/kg) | 3.6 | 2.8 |
(1)黄瓜和茄子各批发了多少kg?
(2)该小组当天卖完这些黄瓜和茄子可赚多少钱?
参考答案:
【答案】(1)黄瓜批发了25kg,茄子批发了15kg;(2)可赚42元.
【解析】
(1)设他当天购进黄瓜x千克,茄子y千克,根据黄瓜的批发价是2.4元,茄子批发价是2元,共花了90元,列出方程,求出x的值,即可求出答案;
(2)根据黄瓜和茄子的斤数,再求出每斤黄瓜和茄子赚的钱数,即可求出总的赚的钱数.
(1)设黄瓜批发了xkg,茄子批发了ykg,
根据题意,得![]() ,
,
解得![]() ,
,
答:黄瓜批发了25kg,茄子批发了15kg.
(2)(3.6﹣2.4)×25+(2.8﹣2)×15=42(元).
答:该小组当天卖完这些黄瓜和茄子可赚42元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:已知二次函数的图象与
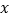 轴交于
轴交于 和
和 两点.交
两点.交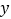 轴于点
轴于点 ,点
,点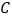 ,
,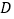 是二次函数图象上的一对对称点,一次函数的图象过点
是二次函数图象上的一对对称点,一次函数的图象过点 ,
,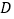
(1)画出图象,并求二次函数的解析式.
(2)根据图象直接写出使一次函数值大于或等于二次函数值的
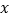 的取值范围.
的取值范围.(3)若直线与
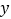 轴交点为
轴交点为 ,连接
,连接 ,
, ,求三角形
,求三角形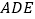 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=50°,CE为△ABC的角平分线,AC边上的高BD与CE所在的直线交于点F,若∠ABD:∠ACF=3:5,则∠BEC的度数为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
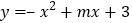 与
与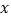 轴的一个交点
轴的一个交点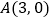 .
.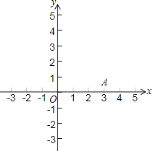
(1)试分别求出这条抛物线与
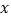 轴的另一个交点
轴的另一个交点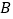 及与
及与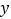 轴的交点
轴的交点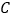 的坐标.
的坐标.(2)设抛物线的顶点为
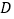 ,请在图中画出抛物线的草图,若点
,请在图中画出抛物线的草图,若点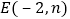 在直线
在直线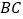 上,试判断
上,试判断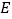 点是否在经过
点是否在经过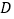 点的反比例函数的图象上,并说明理由;
点的反比例函数的图象上,并说明理由;(3)试求
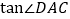 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某食品零售店为食品厂代销一种面包,未售出的面包可以退回厂家.经统计销售情况发现,当这种面包的销售单价为7角时,每天卖出160个.在此基础上.单价每提高1角时,该零售店每天就会少卖出20个面包.设这种面包的销售单价为x角(每个面包的成本是5角).零售店每天销售这种面包的利润为y角.
(1)用含x的代数式分别表示出每个面包的利润与卖出的面包个数;
(2)求x与y之间的函数关系式:
(3)当这种面包的销售单价定为多少时,该零售店每天销售这种面包获得的利润最大?最大利润为多少元?
-
科目: 来源: 题型:
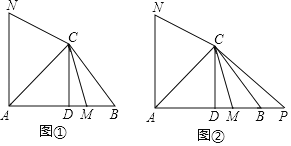
查看答案和解析>>【题目】在△ABC中,∠BAC=45°,CD⊥AB,垂足为点D,M为线段DB上一动点(不包括端点),点N在直线AC左上方且∠NCM=135°,CN=CM,如图①.
(1)求证:∠ACN=∠AMC;
(2)记△ANC得面积为5,记△ABC得面积为5.求证:
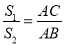 ;
;(3)延长线段AB到点P,使BP=BM,如图②.探究线段AC与线段DB满足什么数量关系时对于满足条件的任意点M,AN=CP始终成立?(写出探究过程)
-
科目: 来源: 题型:
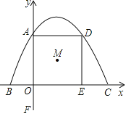
查看答案和解析>>【题目】如图所示,平面直角坐标系中,抛物线
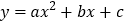 经过
经过 、
、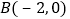 、
、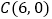 .过点
.过点 作
作 轴交抛物线于点
轴交抛物线于点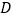 ,过点
,过点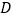 作
作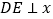 轴,垂足为点
轴,垂足为点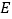 .点
.点 是四边形
是四边形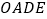 的对角线的交点,点
的对角线的交点,点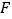 在
在 轴负半轴上,且
轴负半轴上,且 .
.
(1)求抛物线的解析式,并直接写出四边形
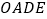 的形状;
的形状; (2)当点
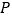 、
、 从
从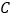 、
、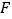 两点同时出发,均以每秒
两点同时出发,均以每秒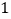 个长度单位的速度沿
个长度单位的速度沿 、
、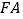 方向运动,点
方向运动,点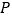 运动到
运动到 时
时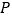 、
、 两点同时停止运动.设运动的时间为
两点同时停止运动.设运动的时间为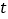 秒,在运动过程中,以
秒,在运动过程中,以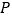 、
、 、
、 、
、 四点为顶点的四边形的面积为
四点为顶点的四边形的面积为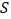 ,求出
,求出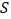 与
与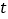 之间的函数关系式,并写出自变量的取值范围;
之间的函数关系式,并写出自变量的取值范围;(3)在抛物线上是否存在点
 ,使以
,使以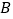 、
、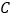 、
、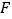 、
、 为顶点的四边形是梯形?若存在,直接写出点
为顶点的四边形是梯形?若存在,直接写出点 的坐标;不存在,说明理由.
的坐标;不存在,说明理由.
相关试题

