【题目】在平面直角坐标系中,一次函数y![]() x+4的图象与x轴和y轴分别交于A、B两点.动点P从点A出发,在线段AO上以每秒1个单位长度的速度向点O作匀速运动,到达点O即停止运动.其中A、Q两点关于点P对称,以线段PQ为边向上作正方形PQMN.设运动时间为秒.如图①.
x+4的图象与x轴和y轴分别交于A、B两点.动点P从点A出发,在线段AO上以每秒1个单位长度的速度向点O作匀速运动,到达点O即停止运动.其中A、Q两点关于点P对称,以线段PQ为边向上作正方形PQMN.设运动时间为秒.如图①.
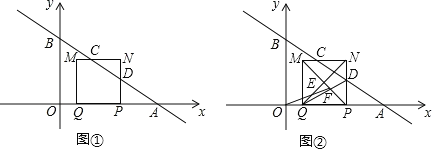
(1)当t=2秒时,OQ的长度为 ;
(2)设MN、PN分别与直线y![]() x+4交于点C、D,求证:MC=NC;
x+4交于点C、D,求证:MC=NC;
(3)在运动过程中,设正方形PQMN的对角线交于点E,MP与QD交于点F,如图2,求OF+EN的最小值.
参考答案:
【答案】(1)2;(2)证明见解析;(3)![]() .
.
【解析】
(1)解方程得到OA=6,由t=2,于是得到结论;
(2)根据AP=PQ=t,得到OQ=6-2t,根据正方形的性质得到PQ=QM=MN=PN=t,求得M(6-2t,t),N(6-t,t),C(6-![]() t,t),求得CM=(6-
t,t),求得CM=(6-![]() t)-(6-2t)=
t)-(6-2t)=![]() t,CN=(6-t)-(6-
t,CN=(6-t)-(6-![]() t)=
t)=![]() t,于是得到结论;
t,于是得到结论;
(3)作矩形NEFK,则EN=FK,推出当O,F,K三点共线时,OF+EN=OF+FK的值最小,如图,作OH⊥QN于H,解直角三角形即可得到结论.
(1)在y![]() x+4中,令y=0,得x=6,∴OA=6.
x+4中,令y=0,得x=6,∴OA=6.
∵t=2,∴AP=PQ=2,
∴OQ=6﹣2﹣2=2.
故答案为:2;
(2)∵AP=PQ=t,∴OQ=6﹣2t.
∵四边形PQMN是正方形,
∴PQ=QM=MN=PN=t,
∴M(6﹣2t,t),N(6﹣t,t),C(6![]() t,t),
t,t),
∴CM=(6![]() t)﹣(6﹣2t)
t)﹣(6﹣2t)![]() t,
t,
CN=(6﹣t)﹣(6![]() t)
t)![]() t,
t,
∴CM=CN;
(3)作矩形NEFK,则EN=FK.
∵OF+EN=OF+FK,
∴当O,F,K三点共线时,OF+EN=OF+FK的值最小,如图,
作OH⊥QN于H,
在等腰直角三角形PQN中,∵PQ=t,∴QN![]() t,
t,
∴HN=QN﹣QH![]() t﹣(
t﹣(![]() t﹣3
t﹣3![]() )=3
)=3![]() ,
,
∴OF+EN的最小值为:HE+EN=HN=3![]() .
.
-
科目: 来源: 题型:
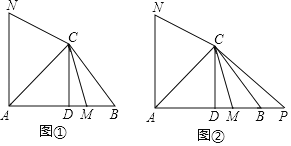
查看答案和解析>>【题目】在△ABC中,∠BAC=45°,CD⊥AB,垂足为点D,M为线段DB上一动点(不包括端点),点N在直线AC左上方且∠NCM=135°,CN=CM,如图①.
(1)求证:∠ACN=∠AMC;
(2)记△ANC得面积为5,记△ABC得面积为5.求证:
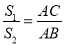 ;
;(3)延长线段AB到点P,使BP=BM,如图②.探究线段AC与线段DB满足什么数量关系时对于满足条件的任意点M,AN=CP始终成立?(写出探究过程)
-
科目: 来源: 题型:
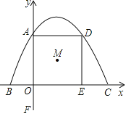
查看答案和解析>>【题目】如图所示,平面直角坐标系中,抛物线
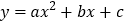 经过
经过 、
、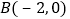 、
、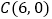 .过点
.过点 作
作 轴交抛物线于点
轴交抛物线于点 ,过点
,过点 作
作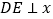 轴,垂足为点
轴,垂足为点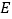 .点
.点 是四边形
是四边形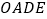 的对角线的交点,点
的对角线的交点,点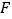 在
在 轴负半轴上,且
轴负半轴上,且 .
.
(1)求抛物线的解析式,并直接写出四边形
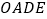 的形状;
的形状; (2)当点
 、
、 从
从 、
、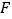 两点同时出发,均以每秒
两点同时出发,均以每秒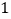 个长度单位的速度沿
个长度单位的速度沿 、
、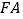 方向运动,点
方向运动,点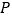 运动到
运动到 时
时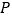 、
、 两点同时停止运动.设运动的时间为
两点同时停止运动.设运动的时间为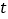 秒,在运动过程中,以
秒,在运动过程中,以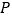 、
、 、
、 、
、 四点为顶点的四边形的面积为
四点为顶点的四边形的面积为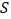 ,求出
,求出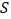 与
与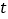 之间的函数关系式,并写出自变量的取值范围;
之间的函数关系式,并写出自变量的取值范围;(3)在抛物线上是否存在点
 ,使以
,使以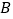 、
、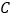 、
、 、
、 为顶点的四边形是梯形?若存在,直接写出点
为顶点的四边形是梯形?若存在,直接写出点 的坐标;不存在,说明理由.
的坐标;不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示经过原点,给出以下四个结论:①abc=0,②a+b+c>0,③2a>b,④4ac﹣b2<0;其中正确的结论有( )
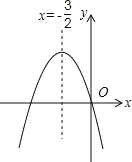
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为________.
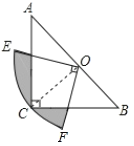
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△POQ中,OP=OQ=4,M是PQ中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.求证:MA=MB;

-
科目: 来源: 题型:
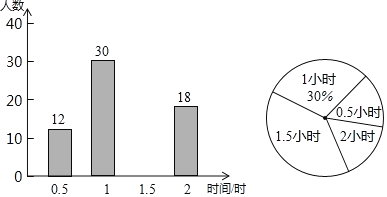
查看答案和解析>>【题目】2019年8月,第18届世界警察和消防员运动会在成都举行.我们在体育馆随机调查了部分市民当天的观赛时间,并用得到的数据绘制了如下不完整的统计图,根据图中信息完成下列问题:
(1)将条形统计图补充完整;
(2)求抽查的市民观赛时间的众数、中位数;
(3)求所有被调查市民的平均观赛时间.
相关试题

