【题目】已知:如图,二次函数y=a(x﹣h)2+![]() 的图象经过原点O(0,0),A(2,0).
的图象经过原点O(0,0),A(2,0).

(1)写出该函数图象的对称轴;
(2)若将线段OA绕点O逆时针旋转60°到OA′,试判断点A′是否为该函数图象的顶点?请说明理由.
参考答案:
【答案】(1)直线x=1 (2)点A′为抛物线y=﹣![]() (x﹣1)2+
(x﹣1)2+![]() 的顶点
的顶点
【解析】
试题分析:(1)把已知点O、A代入函数的解析式可求出h的值h=1,及a=![]() ,然后根据二次函数的顶点式的特点判断出对称轴;
,然后根据二次函数的顶点式的特点判断出对称轴;
(2)由线段OA绕点O逆时针旋转60°到OA′,可知OA′=OA=2,∠A′OA=60°,如图,作A′B⊥x轴于点B,根据直角三角形的特点可知sin60°=![]() ,cos60°=
,cos60°=![]() ,因此可求得A′B=OA′sin60°=
,因此可求得A′B=OA′sin60°=![]() =
=![]() ,OB=OA′cos60°=
,OB=OA′cos60°=![]() =1,所以A′点的坐标为(1,
=1,所以A′点的坐标为(1,![]() ),点A′正好是二次函数y=﹣
),点A′正好是二次函数y=﹣![]() (x﹣1)2+
(x﹣1)2+![]() 的顶点.
的顶点.
试题解析:解:(1)∵二次函数y=a(x﹣h)2+![]() 的图象经过原点O(0,0),A(2,0).
的图象经过原点O(0,0),A(2,0).
∴抛物线的对称轴为直线x=1;
点A′是该函数图象的顶点.理由如下:

如图,作A′B⊥x轴于点B
∵线段OA绕点O逆时针旋转60°到OA′,
∴OA′=OA=2,∠A′OA=60°,
在Rt△A′OB中,
A′B=OA′sin60°=![]() =
=![]() ,
,
∴OB=OA′cos60°=![]() =1.
=1.
∴A′点的坐标为(1,![]() ),
),
∴点A′为抛物线y=﹣![]() (x﹣1)2+
(x﹣1)2+![]() 的顶点.
的顶点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC,点A的坐标是(4,0),点B的坐标是(2,3),点C在x轴的负半轴上,且AC=6.
(1)直接写出点C的坐标.
(2)在y轴上是否存在点P,使得S△POB=
 S△ABC若存在,求出点P的坐标;若不存在,请说明理由.
S△ABC若存在,求出点P的坐标;若不存在,请说明理由.(3)把点C往上平移3个单位得到点H,作射线CH,连接BH,点M在射线CH上运动(不与点C、H重合).试探究∠HBM,∠BMA,∠MAC之间的数量关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个正方形甲和两个正方形乙分别沿着图中虚线川剪刀剪成4个完全相等的长方形和一个正方形(如图1),已知正方形甲中剪出的小正方形面积是1,正方形乙中剪出的小正方形面积是4,现将剪得的12个长方形摆成如图2正方形
 (不重叠无缝隙).则正方形
(不重叠无缝隙).则正方形 的面积是()
的面积是()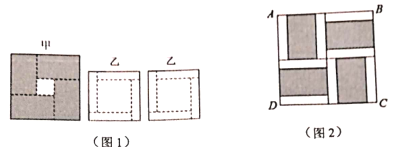
A.9B.16C.25D.36
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
, ,求
,求 的度数.
的度数. 
(1)填空,在空白处填上结果或者理由.
解:过点
 作
作 ,(如图)
,(如图)得
 ___________°, ( )
___________°, ( )又因为
 ,(已知)
,(已知)所以
 ___________°.
___________°. 因为
 ,
,所以
 , ( )
, ( )又因为
 ,(已知)
,(已知)所以
 ___________°,
___________°,所以
 ___________°.
___________°. (2)请用另一种解法求
 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点
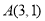 ,
,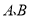 两点关于原点对称,将点
两点关于原点对称,将点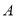 向左平移3个单位到达点
向左平移3个单位到达点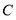 ,设点
,设点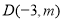 ,且
,且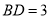 .
. 
(1)求实数
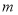 的值;
的值;(2)画出以点
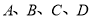 为顶点的四边形,并求出这个四边形的面积.
为顶点的四边形,并求出这个四边形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,H是△ABC的高AD,BE的交点,且DH=DC,则下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
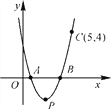
查看答案和解析>>【题目】如图,抛物线y=ax2-5ax+4a与x轴相交于点A,B,且过点C(5,4).
(1)求a的值和该抛物线顶点P的坐标;
(2)请你设计一种平移的方法,使平移后抛物线的顶点落在第二象限,并写出平移后抛物线的表达式.
相关试题

