【题目】如图所示,H是△ABC的高AD,BE的交点,且DH=DC,则下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】B
【解析】解:①∵BE⊥AC,AD⊥BC,∴∠AEH=∠ADB=90°.
∵∠HBD+∠BHD=90°,∠EAH+∠AHE=90°,∠BHD=∠AHE,∴∠HBD=∠EAH.
∵DH=DC,∴△BDH≌△ADC(AAS),∴BD=AD,BH=AC;
②∵BC=AC,∴∠BAC=∠ABC.
由①知,在Rt△ABD中,∵BD=AD,∴∠ABC=45°,∴∠BAC=45°,∴∠ACB=90°.
∵∠ACB+∠DAC=90°,∠ACB<90°,∴结论②为错误结论.
③由①证明知,△BDH≌△ADC,∴BH=AC;
④∵CE=CD,∠ACB=∠ACB;∠ADC=∠BEC=90°,∴△BEC≌△ADC,由于缺乏条件,无法证得△BEC≌△ADC,∴结论④为错误结论.
综上所述,结论①,③为正确结论,结论②,④为错误结论,根据题意故选B.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
, ,求
,求 的度数.
的度数. 
(1)填空,在空白处填上结果或者理由.
解:过点
 作
作 ,(如图)
,(如图)得
 ___________°, ( )
___________°, ( )又因为
 ,(已知)
,(已知)所以
 ___________°.
___________°. 因为
 ,
,所以
 , ( )
, ( )又因为
 ,(已知)
,(已知)所以
 ___________°,
___________°,所以
 ___________°.
___________°. (2)请用另一种解法求
 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,二次函数y=a(x﹣h)2+
 的图象经过原点O(0,0),A(2,0).
的图象经过原点O(0,0),A(2,0).
(1)写出该函数图象的对称轴;
(2)若将线段OA绕点O逆时针旋转60°到OA′,试判断点A′是否为该函数图象的顶点?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点
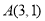 ,
,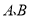 两点关于原点对称,将点
两点关于原点对称,将点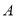 向左平移3个单位到达点
向左平移3个单位到达点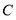 ,设点
,设点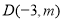 ,且
,且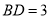 .
. 
(1)求实数
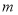 的值;
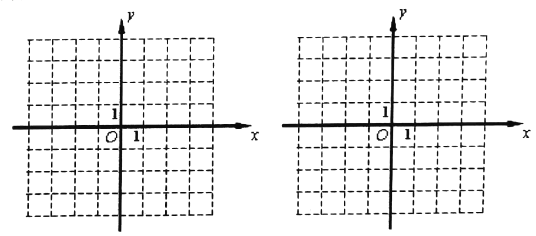
的值;(2)画出以点
 为顶点的四边形,并求出这个四边形的面积.
为顶点的四边形,并求出这个四边形的面积. -
科目: 来源: 题型:
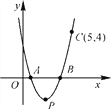
查看答案和解析>>【题目】如图,抛物线y=ax2-5ax+4a与x轴相交于点A,B,且过点C(5,4).
(1)求a的值和该抛物线顶点P的坐标;
(2)请你设计一种平移的方法,使平移后抛物线的顶点落在第二象限,并写出平移后抛物线的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下说法合理的是( )
A. 小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是
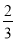
B. 某彩票的中奖概率是5%,那么买100张彩票一定有5张中奖
C. 某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是
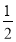
D. 小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率还是
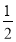
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果二次函数的二次项系数为1,那么此二次函数可表示为y=x2+px+q,我们称[p,q]为此函数的特征数,如函数y=x2+2x+3的特征数是[2,3].
(1)若一个函数的特征数为[-2,1],求此函数图象的顶点坐标;
(2)探究下列问题:
①若一个函数的特征数为[4,-1],将此函数的图象先向右平移1个单位长度,再向上平移1个单位长度,求得到的图象对应的函数的特征数;
②若一个函数的特征数为[2,3],问此函数的图象经过怎样的平移,才能使得到的图象对应的函数的特征数为[3,4]?
相关试题

