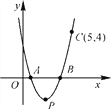
【题目】如图,抛物线y=ax2-5ax+4a与x轴相交于点A,B,且过点C(5,4).
(1)求a的值和该抛物线顶点P的坐标;
(2)请你设计一种平移的方法,使平移后抛物线的顶点落在第二象限,并写出平移后抛物线的表达式.
参考答案:
【答案】(1) (![]() ,-
,- ![]() );(2)答案不唯一,合理即可,y=x2+x+2.
);(2)答案不唯一,合理即可,y=x2+x+2.
【解析】试题分析:将点c坐标代入函数表达式即可求出a的值,a=1,将函数表达式转换为顶点式y=x2-5x+4=(x-![]() )2-
)2-![]() ,所以顶点坐标是(
,所以顶点坐标是(![]() ,-
,- ![]() );将抛物线平移后顶点在第二象限,答案不唯一,可通过平移顶点,例如先向左平移3个单位长度,则变为y= (x-
);将抛物线平移后顶点在第二象限,答案不唯一,可通过平移顶点,例如先向左平移3个单位长度,则变为y= (x-![]() )2-
)2-![]() ,再向上平移4个单位,得到y= (x-
,再向上平移4个单位,得到y= (x-![]() )2-
)2-![]() +4= (x+
+4= (x+![]() )2+
)2+![]() = x2+x+2.
= x2+x+2.
解:(1)把点C(5,4)代入抛物线y=ax2-5ax+4a,得25a-25a+4a=4.解得a=1.
∴二次函数的表达式为y=x2-5x+4.
∵y=x2-5x+4=(x-![]() )2-
)2-![]() ,
,
∴顶点P的坐标为(![]() ,-
,- ![]() ).
).
(2)答案不唯一,合理即可,如:先向左平移3个单位长度,再向上平移4个单位长度,得到的二次函数表达式为y=(x-![]() +3)2-
+3)2-![]() +4=(x+
+4=(x+![]() )2+
)2+![]() ,
,
即y=x2+x+2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,二次函数y=a(x﹣h)2+
 的图象经过原点O(0,0),A(2,0).
的图象经过原点O(0,0),A(2,0).
(1)写出该函数图象的对称轴;
(2)若将线段OA绕点O逆时针旋转60°到OA′,试判断点A′是否为该函数图象的顶点?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点
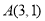 ,
,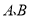 两点关于原点对称,将点
两点关于原点对称,将点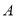 向左平移3个单位到达点
向左平移3个单位到达点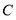 ,设点
,设点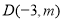 ,且
,且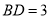 .
. 
(1)求实数
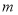 的值;
的值;(2)画出以点
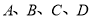 为顶点的四边形,并求出这个四边形的面积.
为顶点的四边形,并求出这个四边形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,H是△ABC的高AD,BE的交点,且DH=DC,则下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下说法合理的是( )
A. 小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是
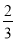
B. 某彩票的中奖概率是5%,那么买100张彩票一定有5张中奖
C. 某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是
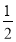
D. 小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率还是
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果二次函数的二次项系数为1,那么此二次函数可表示为y=x2+px+q,我们称[p,q]为此函数的特征数,如函数y=x2+2x+3的特征数是[2,3].
(1)若一个函数的特征数为[-2,1],求此函数图象的顶点坐标;
(2)探究下列问题:
①若一个函数的特征数为[4,-1],将此函数的图象先向右平移1个单位长度,再向上平移1个单位长度,求得到的图象对应的函数的特征数;
②若一个函数的特征数为[2,3],问此函数的图象经过怎样的平移,才能使得到的图象对应的函数的特征数为[3,4]?
-
科目: 来源: 题型:
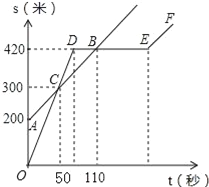
查看答案和解析>>【题目】某中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动朱老师先跑,当小明出发时,朱老师已经距起点200米了,他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).根据图中给出的信息,解答下列问题:
(1)在上述变化过程中,自变量是 ,因变量是 ;
(2)朱老师的速度为 米/秒;小明的速度为 米/秒;
(3)小明与朱老师相遇 次,相遇时距起点的距离分别为 米.
相关试题

