【题目】如图,已知直线y=﹣x和反比例函数 ![]() (k>0),点A(m,n)(m>0)在反比例函数
(k>0),点A(m,n)(m>0)在反比例函数![]() 上.
上.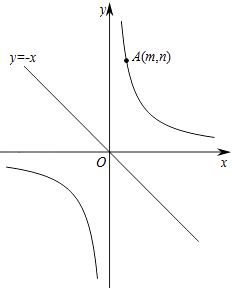
(1)当m=n=2时,
①直接写出k的值;
②将直线y=﹣x作怎样的平移能使平移后的直线与反比例函数 ![]() 只有一个交点.
只有一个交点.
(2)将直线y=﹣x绕着原点O旋转,设旋转后的直线与反比例函数 ![]() 交于点B(a,b)(a>0,b>0)和点C.设直线AB,AC分别与x轴交于D,E两点,试问:
交于点B(a,b)(a>0,b>0)和点C.设直线AB,AC分别与x轴交于D,E两点,试问: ![]() 与
与 ![]() 的值存在怎样的数量关系?请说明理由.
的值存在怎样的数量关系?请说明理由.
参考答案:
【答案】
(1)
解:①当m=n=2时,A(2,2),
把点A(2,2)代入反比例函数 ![]() (k>0)得:k=2×2=4;
(k>0)得:k=2×2=4;
②设平移后的直线解析式为y=﹣x+b1,
由 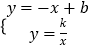 可得,
可得, ![]() ,
,
整理可得:x2﹣b1x+4=0,
当 ![]() ,即b1=±4时,方程x2﹣b1x+4=0有两个相等的实数根,此时直线y=﹣x+b1与反比例函数只有一个交点,
,即b1=±4时,方程x2﹣b1x+4=0有两个相等的实数根,此时直线y=﹣x+b1与反比例函数只有一个交点,
∴只要将直线y=﹣x向上或向下平移4个单位长度,所得到的直线与反比例函数只有一个交点
(2)
解: ![]() ,理由如下:
,理由如下:
分两种情况讨论:由反比例函数的对称性可知,C(﹣a,﹣b)
①当点A在直线BC的上方时,如图所示:
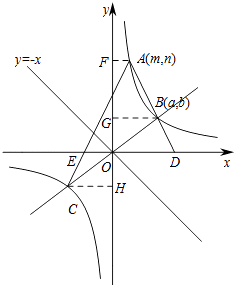
过A、B、C分别作y轴的垂线,垂足分别为F、G、H,
则OF=n,OG=OH=b,
∴FG=OF﹣OG=n﹣b,FH=OF+OH=n+b,
∵AF∥BG∥x轴,
∴ ![]() =
= ![]() =
= ![]() ,
,
∵AF∥x轴∥CH,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() +
+ ![]() =
= ![]() +
+ ![]() =2;
=2;
②当点A在直线BC的下方时,
同理可求: ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴ ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() =2;
=2;
综上所述, ![]() .
.
【解析】(1)①当m=n=2时,得出A(2,2),把点A(2,2)代入双曲线 ![]() (k>0)求出k的值即可;
(k>0)求出k的值即可;
②设平移后的直线解析式为y=﹣x+b1 , 由直线和双曲线解析式组成方程组,整理可得方程:x2﹣b1x+4=0,当判别式=0时,求出b1=±4即可;(2)分两种情况讨论:由双曲线的对称性可知,C(﹣a,﹣b),①当点A在直线BC的上方时,过A、B、C分别作y轴的垂线,垂足分别为F、G、H,则OF=n,OG=OH=b,得出FG=OF﹣OG=n﹣b,FH=OF+OH=n+b,由平行线得出比例式,即可得出结论;
②当点A在直线BC的下方时,同理可得出结论;即可得出结果.
【考点精析】解答此题的关键在于理解反比例函数的图象的相关知识,掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列二元一次方程组
(1)
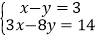
(2)
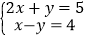
(3)
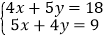
(4)
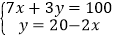
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,我国很多地区持续出现雾霾天气.某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表:

组别
观点
频数(人数)
A
大气气压低,空气不流动
m
B
地面灰尘大,空气湿度低
40
C
汽车尾气排放
n
D
工厂造成的污染
120
E
其他
60
请根据图表中提供的信息解答下列问题:
(1)填空:m= ,n= ,扇形统计图中E组所占的百分比为 % ;
(2)若该市人口约有400万人,请你计算其中持D组“观点”的市民人数;
(3)对于“雾霾”这个环境问题,请用简短的语言发出倡议.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在温度不变的条件下,一定质量的气体的压强p与它的体积V成反比例,当V=200时,p=50,则当p=25时,V= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=3x+6与两坐标轴围成的三角形的面积为( )
A.6
B.12
C.3
D.24 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
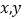 的方程组
的方程组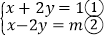 ,
,(1)若用代入法求解,可由①得:
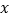 = ③,把③代入②解得
= ③,把③代入②解得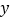 = ,将其代入③解得
= ,将其代入③解得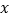 = ,∴原方程组的解为 ;
= ,∴原方程组的解为 ;(2)若此方程组的解
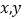 互为相反数,求这个方程组的解及
互为相反数,求这个方程组的解及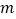 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】要比较两名同学共六次数学测试中谁的成绩比较稳定,应选用的统计量为( )
A. 中位数 B. 方差 C. 平均数 D. 众数
相关试题

