【题目】为了测量出大楼AB的高度,从距离楼底B处50米的点C(点C与楼底B在同一水平面上)出发,沿倾斜角为30°的斜坡CD前进20米到达点D,在点D处测得楼顶A的仰角为64°,求大楼AB的高度(结果精确到1米)(参考数据:sin64°≈0.9,cos64°≈0.4,tan64°≈2.1, ![]() ≈1.7)
≈1.7)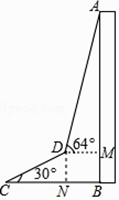
参考答案:
【答案】解:在Rt△CDN中,∵CD=20米,∠C=30°,
∴BM=DN= ![]() CD=10米,CN=CDcos∠C=20×
CD=10米,CN=CDcos∠C=20× ![]() =10
=10 ![]() 米,
米,
∵BC=50米,
∴DM=BN=BC﹣CN=50﹣10 ![]() ,
,
在Rt△ADN中,由tan∠ADN= ![]() 可得AM=DMtan∠ADN=(50﹣10
可得AM=DMtan∠ADN=(50﹣10 ![]() )tan64°,
)tan64°,
则AB=AM+BM=(50﹣10 ![]() )tan64°+10≈79米,
)tan64°+10≈79米,
答:楼AB的高度约为79米.
【解析】在Rt△CDN中求得BM=DN= ![]() CD=10、CN=CDcos∠C=10
CD=10、CN=CDcos∠C=10 ![]() ,即可知DM=BN=50﹣10
,即可知DM=BN=50﹣10 ![]() ,根据AB=BM+AM=BM+DMtan∠ADN可得答案.
,根据AB=BM+AM=BM+DMtan∠ADN可得答案.
【考点精析】通过灵活运用关于仰角俯角问题,掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个仓库共存有粮食60
 .解决下列问题,3个小题都要写出必要的解题过程:
.解决下列问题,3个小题都要写出必要的解题过程:(1)甲仓库运进粮食14
 ,乙仓库运出粮食10
,乙仓库运出粮食10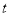 后,两个仓库的粮食数量相等.甲、乙两个仓库原来各有多少粮食?
后,两个仓库的粮食数量相等.甲、乙两个仓库原来各有多少粮食?(2)如果甲仓库原有的粮食比乙仓库的2倍少3
 ,则甲仓库运出多少
,则甲仓库运出多少 粮食给乙仓库,可使甲、乙两仓库粮食数量相等?
粮食给乙仓库,可使甲、乙两仓库粮食数量相等? (3)甲乙两仓库同时运进粮食,甲仓库运进的数量比本仓库原存粮食数量的一半多1
 ,乙仓库运进的数量是本仓库原有粮食数量加上8
,乙仓库运进的数量是本仓库原有粮食数量加上8 所得的和的一半.求此时甲、乙两仓库共有粮食多少
所得的和的一半.求此时甲、乙两仓库共有粮食多少 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°, D是AB边上一点,且DB=DC,过BC上一点P(不包括B,C二点)作PE⊥AB,垂足为点E, PF⊥CD,垂足为点F,已知AD:DB=1:4,BC=
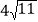 ,求PE+PF的长.
,求PE+PF的长.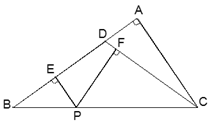
-
科目: 来源: 题型:
查看答案和解析>>【题目】网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,为了解市民对售后评价的关注情况,随机采访部分市民,对采访情况制作了如下统计图表:
关注情况
频数
频率
A.高度关注
50
b
B.一般关注
120
0.6
C.不关注
a
0.1
D.不知道
10
0.05
(1)根据上述统计图可得此次采访的人数为人,a= , b=;
(2)根据以上信息补全条形统计图;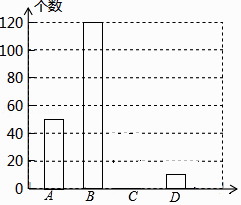
(3)根据上述采访结果,请估计在6400名市民中,高度关注售后评价的市民约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,六边形ABCDEF的内角都相等,∠DAB=60°,AB=DE,则下列结论成立的个数是( )
①AB∥DE;②EF∥AD∥BC;③AF=CD;④四边形ACDF是平行四边形;⑤六边形ABCDEF既是中心对称图形,又是轴对称图形.

A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】新学期开学,某体育用品商店开展促销活动,有两种优惠方案.
方案一:不购买会员卡时,乒乓球享受8.5折优惠,乒乓球拍购买5副(含5副)以上才能享受8.5折优惠,5副以下必须按标价购买.
方案二:办理会员卡时,全部商品享受八折优惠,小健和小康的谈话内容如下:

会员卡只限本人使用.
(1)求该商店销售的乒乓球拍每副的标价.
(2)如果乒乓球每盒10元,小健需购买乒乓球拍6副,乒乓球a盒,请回答下列问题:
①如果方案一与方案二所付钱数一样多,求a的值;
②直接写出一个恰当的a值,使方案一比方案二优惠;
③直接写出一个恰当的a值,使方案二比方案一优惠.
-
科目: 来源: 题型:
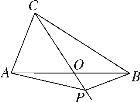
查看答案和解析>>【题目】(题文)如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为________________(提示:直角三角形斜边上的中线等于斜边的一半).
相关试题

