【题目】甲、乙两个仓库共存有粮食60![]() .解决下列问题,3个小题都要写出必要的解题过程:
.解决下列问题,3个小题都要写出必要的解题过程:
(1)甲仓库运进粮食14![]() ,乙仓库运出粮食10
,乙仓库运出粮食10![]() 后,两个仓库的粮食数量相等.甲、乙两个仓库原来各有多少粮食?
后,两个仓库的粮食数量相等.甲、乙两个仓库原来各有多少粮食?
(2)如果甲仓库原有的粮食比乙仓库的2倍少3![]() ,则甲仓库运出多少
,则甲仓库运出多少![]() 粮食给乙仓库,可使甲、乙两仓库粮食数量相等?
粮食给乙仓库,可使甲、乙两仓库粮食数量相等?
(3)甲乙两仓库同时运进粮食,甲仓库运进的数量比本仓库原存粮食数量的一半多1![]() ,乙仓库运进的数量是本仓库原有粮食数量加上8
,乙仓库运进的数量是本仓库原有粮食数量加上8![]() 所得的和的一半.求此时甲、乙两仓库共有粮食多少
所得的和的一半.求此时甲、乙两仓库共有粮食多少![]() ?
?
参考答案:
【答案】(1)原来甲仓库有18t粮食,乙仓库有42t粮食;(2)甲仓库运出9t粮食给乙仓库,可使甲、乙两仓库粮食数量相等(3)甲乙两仓库共存有粮食95t
【解析】试题分析:(1)设甲有xt,则乙有(60-x)t,根据甲仓库运进粮食14t,乙仓库运出粮食10t后,两个仓库的粮食数量相等,可得出方程,解出即可;
(2)先求出甲乙粮仓原有多少粮食,再求甲运出的粮食数量即可;
(3)根据题意列出代数式求值 即可.
试题解析:(1)设甲仓库原有粮食xt,则乙仓库原有粮食(60-x)t,
由题知x+14=(60-x)-10,解得x=18.
当x=18时,60-x=42.
∴原来甲仓库有18t粮食,乙仓库有42t粮食;
(2)设甲仓库原有粮食xt,则乙仓库原有粮食(60-x)t,
由题知x=2(60-x)-3,解得x=39.
当x=39时,60-x=21.
∴原来甲仓库有39t粮食,乙仓库有21t粮食.
设甲仓库运出yt粮食给乙仓库,可使甲、乙两仓库粮食数量相等,
由题知39-y=21+y,解得y=9,
∴甲仓库运出9t粮食给乙仓库,可使甲、乙两仓库粮食数量相等.
(3)设甲仓库原有粮食xt,乙仓库原有粮食yt,则x+y=60.
设运进粮食后,两仓库共有粮食wt,则
w=60+(![]() x+1)+
x+1)+![]() (y+8)=65+
(y+8)=65+![]() (x+y)=65+30=95,
(x+y)=65+30=95,
∴此时甲乙两仓库共存有粮食95t.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=22,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)数轴上点B表示的数 ;点P表示的数 (用含t的代数式表示)
(2)若M为AP的中点,N为BP的中点,在点P运动的过程中,线段MN的长度是 .
(3)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点P、Q同时出发,问多少秒时P、Q之间的距离恰好等于2?
(4)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学活动课上,老师出示两张等腰三角形纸片,如图所示.图1的三角形边长分别为4,4,2;图2的三角形的腰长也为4,底角等于图1中三角形的顶角;某学习小组将这两张纸片在同一平面内拼成如图3的四边形OABC,连结AC.该学习小组经探究得到以下四个结论,其中错误的是( )
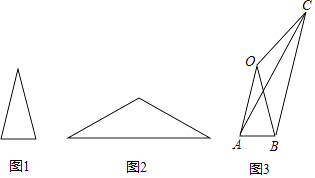
A.∠OCB=2∠ACB
B.∠OAB+∠OAC=90°
C.AC=2
D.BC=4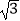
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E、F分别为平行四边形ABCD的对边AD、BC上的点,且DE=BF,EM⊥AC于M,FN⊥AC于N,EF交AC于点O,
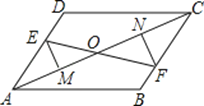
求证:(1)EM=FN;
(2)EF与MN互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点C(0,4),射线CE∥x轴,直线y=﹣
 x+b交线段OC于点B,交x轴于点A,D是射线CE上一点.若存在点D,使得△ABD恰为等腰直角三角形,则b的值为 .
x+b交线段OC于点B,交x轴于点A,D是射线CE上一点.若存在点D,使得△ABD恰为等腰直角三角形,则b的值为 . 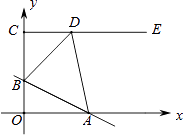
-
科目: 来源: 题型:
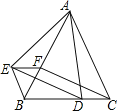
查看答案和解析>>【题目】如图,△ABC和△BEF都是等边三角形,点D在BC边上,点F在AB边上,且∠EAD=60°,连接ED、CF.
(1)求证:△ABE≌△ACD;
(2)求证:四边形EFCD是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒
 个单位长度,则第2018秒时,点P的坐标是( )
个单位长度,则第2018秒时,点P的坐标是( )
A. (2016,0) B. (2017,0) C. (2018,0) D. (2017,1)
相关试题

