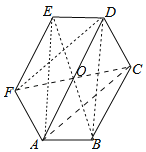
【题目】如图,六边形ABCDEF的内角都相等,∠DAB=60°,AB=DE,则下列结论成立的个数是( )
①AB∥DE;②EF∥AD∥BC;③AF=CD;④四边形ACDF是平行四边形;⑤六边形ABCDEF既是中心对称图形,又是轴对称图形.

A. 2 B. 3 C. 4 D. 5
参考答案:
【答案】D
【解析】试题解析:∵六边形ABCDEF的内角都相等,∴∠EFA=∠FED=∠FAB=∠ABC=120°,∵∠DAB=60°,∴∠DAF=60°,∴∠EFA+∠DAF=180°,∠DAB+∠ABC=180°,∴AD∥EF∥CB,故②正确,∴∠FED+∠EDA=180°,∴∠EDA=∠ADC=60°,∴∠EDA=∠DAB,∴AB∥DE,故①正确,∵∠FAD=∠EDA,∠CDA=∠BAD,EF∥AD∥BC,∴四边形EFAD,四边形BCDA是等腰梯形,∴AF=DE,AB=CD,∵AB=DE,∴AF=CD,故③正确,连接CF与AD交于点O,连接DF、AC、AE、DB、BE.
∵∠CDA=∠DAF,∴AF∥CD,AF=CD,∴四边形AFDC是平行四边形,故④正确,同法可证四边形AEDB是平行四边形,∴AD与CF,AD与BE互相平分,∴OF=OC,OE=OB,OA=OD,∴六边形ABCDEF既是中心对称图形,故⑤正确,故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°, D是AB边上一点,且DB=DC,过BC上一点P(不包括B,C二点)作PE⊥AB,垂足为点E, PF⊥CD,垂足为点F,已知AD:DB=1:4,BC=
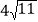 ,求PE+PF的长.
,求PE+PF的长.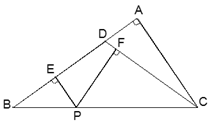
-
科目: 来源: 题型:
查看答案和解析>>【题目】网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,为了解市民对售后评价的关注情况,随机采访部分市民,对采访情况制作了如下统计图表:
关注情况
频数
频率
A.高度关注
50
b
B.一般关注
120
0.6
C.不关注
a
0.1
D.不知道
10
0.05
(1)根据上述统计图可得此次采访的人数为人,a= , b=;
(2)根据以上信息补全条形统计图;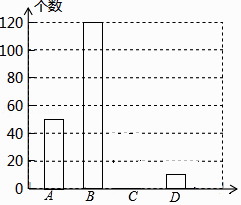
(3)根据上述采访结果,请估计在6400名市民中,高度关注售后评价的市民约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了测量出大楼AB的高度,从距离楼底B处50米的点C(点C与楼底B在同一水平面上)出发,沿倾斜角为30°的斜坡CD前进20米到达点D,在点D处测得楼顶A的仰角为64°,求大楼AB的高度(结果精确到1米)(参考数据:sin64°≈0.9,cos64°≈0.4,tan64°≈2.1,
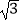 ≈1.7)
≈1.7)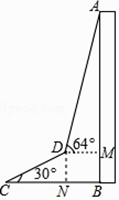
-
科目: 来源: 题型:
查看答案和解析>>【题目】新学期开学,某体育用品商店开展促销活动,有两种优惠方案.
方案一:不购买会员卡时,乒乓球享受8.5折优惠,乒乓球拍购买5副(含5副)以上才能享受8.5折优惠,5副以下必须按标价购买.
方案二:办理会员卡时,全部商品享受八折优惠,小健和小康的谈话内容如下:

会员卡只限本人使用.
(1)求该商店销售的乒乓球拍每副的标价.
(2)如果乒乓球每盒10元,小健需购买乒乓球拍6副,乒乓球a盒,请回答下列问题:
①如果方案一与方案二所付钱数一样多,求a的值;
②直接写出一个恰当的a值,使方案一比方案二优惠;
③直接写出一个恰当的a值,使方案二比方案一优惠.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为________________(提示:直角三角形斜边上的中线等于斜边的一半).
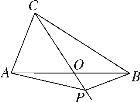
-
科目: 来源: 题型:
查看答案和解析>>【题目】设A=
 ÷(a﹣
÷(a﹣ ).
).(1)化简A;
(2)当a=3时,记此时A的值为f(3);当a=4时,记此时A的值为f(4);…解关于x的不等式:
 ≤f(3)+f(4)+…+f(11),并将解集在数轴上表示出来.
≤f(3)+f(4)+…+f(11),并将解集在数轴上表示出来.
相关试题

