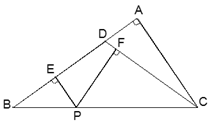
【题目】如图,在△ABC中,∠A=90°, D是AB边上一点,且DB=DC,过BC上一点P(不包括B,C二点)作PE⊥AB,垂足为点E, PF⊥CD,垂足为点F,已知AD:DB=1:4,BC=![]() ,求PE+PF的长.
,求PE+PF的长.
参考答案:
【答案】4![]()
【解析】结合已知AD:DB=1:4,BC=![]() ,应用勾股定理求出AC的长,连接PD,根据S△PBD+S△PCD=S△BCD,可得
,应用勾股定理求出AC的长,连接PD,根据S△PBD+S△PCD=S△BCD,可得![]() BDPE+
BDPE+![]() DCPF=
DCPF=![]() BDAC,继而得到PE+PF=AC即可得.
BDAC,继而得到PE+PF=AC即可得.
∵AD:DB=1:4,
∴设AD=n,BD=4n,
∴AB=5n,
∵DB=DC,∴DC=4n,
∵∠A=90°,∴AC2=DC2-AD2=15n2,AB2+AC2=BC2,
∵BC=4![]() ,
,
∴(5n)2+15n2=![]() ,
,
∴n2=![]() ,∴AC=
,∴AC=![]() =
=![]() ,
,
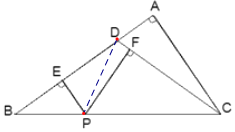
连接PD,PD把△BCD分成两个三角形△PBD,△PCD,
∵PE⊥AB ,PF⊥CD,AC⊥BD,
∴S△PBD=![]() BDPE,
BDPE,
S△PCD=![]() DCPF,
DCPF,
S△BCD=![]() BDAC,
BDAC,
∵S△PBD+S△PCD=S△BCD,
∴![]() BDPE+
BDPE+![]() DCPF=
DCPF=![]() BDAC,
BDAC,
∵DB=DC,
∴PE+PF=AC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)【阅读发现】如图①,在△ABC中,∠ACB=45°,AD⊥BC于点D,E为AD上一点,且DE=BD,可知AB=CE.
(2)【类比探究】如图②,在正方形ABCD中,对角线AC与BD交于点O,E是OC上任意一点,AG⊥BE于点G,交BD于点F.判断AF与BE的数量关系,并加以证明.
(3)【推广应用】在图②中,若AB=4,BF= ,则△AGE的面积为 .
,则△AGE的面积为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】高铁的开通,给N市市民出行带来了极大的方便,“元旦”期间,甲、乙两人应邀到A市的艺术馆参加演出,甲乘私家车从N市出发1小时后,乙乘坐高铁从N市出发,先到A市火车站,然后再转乘出租车到A市的艺术馆(换车时间忽略不计),两人恰好同时到达A市的艺术馆,他们离开N市的距离y(千米)与乘车时间x(小时)的关系如图所示,请结合图象解答下列问题:
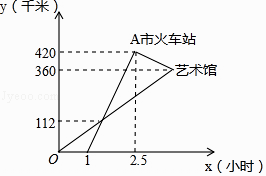
(1)高铁的平均速度是每小时多少千米?
(2)分别求甲、乙(乘坐高铁时)两人离开N市的距离y与乘车时间x的函数关系式;
(3)若甲要提前30分钟到达艺术馆,那么私家车的速度必须达到多少千米/小时? -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个仓库共存有粮食60
 .解决下列问题,3个小题都要写出必要的解题过程:
.解决下列问题,3个小题都要写出必要的解题过程:(1)甲仓库运进粮食14
 ,乙仓库运出粮食10
,乙仓库运出粮食10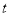 后,两个仓库的粮食数量相等.甲、乙两个仓库原来各有多少粮食?
后,两个仓库的粮食数量相等.甲、乙两个仓库原来各有多少粮食?(2)如果甲仓库原有的粮食比乙仓库的2倍少3
 ,则甲仓库运出多少
,则甲仓库运出多少 粮食给乙仓库,可使甲、乙两仓库粮食数量相等?
粮食给乙仓库,可使甲、乙两仓库粮食数量相等? (3)甲乙两仓库同时运进粮食,甲仓库运进的数量比本仓库原存粮食数量的一半多1
 ,乙仓库运进的数量是本仓库原有粮食数量加上8
,乙仓库运进的数量是本仓库原有粮食数量加上8 所得的和的一半.求此时甲、乙两仓库共有粮食多少
所得的和的一半.求此时甲、乙两仓库共有粮食多少 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,为了解市民对售后评价的关注情况,随机采访部分市民,对采访情况制作了如下统计图表:
关注情况
频数
频率
A.高度关注
50
b
B.一般关注
120
0.6
C.不关注
a
0.1
D.不知道
10
0.05
(1)根据上述统计图可得此次采访的人数为人,a= , b=;
(2)根据以上信息补全条形统计图;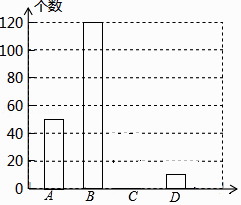
(3)根据上述采访结果,请估计在6400名市民中,高度关注售后评价的市民约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了测量出大楼AB的高度,从距离楼底B处50米的点C(点C与楼底B在同一水平面上)出发,沿倾斜角为30°的斜坡CD前进20米到达点D,在点D处测得楼顶A的仰角为64°,求大楼AB的高度(结果精确到1米)(参考数据:sin64°≈0.9,cos64°≈0.4,tan64°≈2.1,
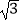 ≈1.7)
≈1.7)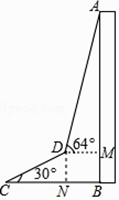
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,六边形ABCDEF的内角都相等,∠DAB=60°,AB=DE,则下列结论成立的个数是( )
①AB∥DE;②EF∥AD∥BC;③AF=CD;④四边形ACDF是平行四边形;⑤六边形ABCDEF既是中心对称图形,又是轴对称图形.

A. 2 B. 3 C. 4 D. 5
相关试题

