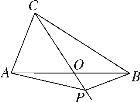
【题目】(题文)如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为________________(提示:直角三角形斜边上的中线等于斜边的一半).
参考答案:
【答案】![]()
【解析】利用分类讨论,当∠ABP=90°时,如图2,由对顶角的性质可得∠AOC=∠BOP=60°,易得∠BPO=30°,易得BP的长,利用勾股定理可得AP的长;当∠APB=90°时,分两种情况讨论,情况一:如图1,利用直角三角形斜边的中线等于斜边的一半得出PO=BO,易得△BOP为等边三角形,利用锐角三角函数可得AP的长;易得BP,利用勾股定理可得AP的长;情况二:如图3,利用直角三角形斜边的中线等于斜边的一半可得结论.
当∠ABP=90°时(如图2).
∵∠AOC=∠BOP=60°,∴∠BPO=30°,∴BP=![]() =
=![]() =2
=2![]() ,在直角三角形ABP中,AP=
,在直角三角形ABP中,AP=![]() =2
=2![]() ,
,
当∠APB=90°时,分两种情况讨论:
情况一:(如图1).
∵AO=BO,∴PO=BO.
∵∠AOC=60°,∴∠BOP=60°,∴△BOP为等边三角形.
∵AB=BC=4,∴AP=ABsin60°=4×![]() =2
=2![]() ;
;
情况二:如图3.
∵AO=BO,∠APB=90°,∴PO=AO.
∵∠AOC=60°,∴△AOP为等边三角形,∴AP=AO=2.
故答案为:2![]() 或2
或2![]() 或2.
或2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了测量出大楼AB的高度,从距离楼底B处50米的点C(点C与楼底B在同一水平面上)出发,沿倾斜角为30°的斜坡CD前进20米到达点D,在点D处测得楼顶A的仰角为64°,求大楼AB的高度(结果精确到1米)(参考数据:sin64°≈0.9,cos64°≈0.4,tan64°≈2.1,
 ≈1.7)
≈1.7)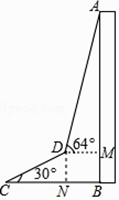
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,六边形ABCDEF的内角都相等,∠DAB=60°,AB=DE,则下列结论成立的个数是( )
①AB∥DE;②EF∥AD∥BC;③AF=CD;④四边形ACDF是平行四边形;⑤六边形ABCDEF既是中心对称图形,又是轴对称图形.

A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】新学期开学,某体育用品商店开展促销活动,有两种优惠方案.
方案一:不购买会员卡时,乒乓球享受8.5折优惠,乒乓球拍购买5副(含5副)以上才能享受8.5折优惠,5副以下必须按标价购买.
方案二:办理会员卡时,全部商品享受八折优惠,小健和小康的谈话内容如下:

会员卡只限本人使用.
(1)求该商店销售的乒乓球拍每副的标价.
(2)如果乒乓球每盒10元,小健需购买乒乓球拍6副,乒乓球a盒,请回答下列问题:
①如果方案一与方案二所付钱数一样多,求a的值;
②直接写出一个恰当的a值,使方案一比方案二优惠;
③直接写出一个恰当的a值,使方案二比方案一优惠.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设A=
 ÷(a﹣
÷(a﹣ ).
).(1)化简A;
(2)当a=3时,记此时A的值为f(3);当a=4时,记此时A的值为f(4);…解关于x的不等式:
 ≤f(3)+f(4)+…+f(11),并将解集在数轴上表示出来.
≤f(3)+f(4)+…+f(11),并将解集在数轴上表示出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC,过AD的中点O作EF⊥AD,分别交AB、AC于点E、F,连接DE、DF.
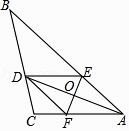
(1)判断四边形AFDE是什么四边形?请说明理由;
(2)若BD=8,CD=3,AE=4,求CF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】煤气公司一工人检修一条长540米的煤气管道,计划用若干小时完成,在实际检修过程中,每小时检修的管道长度是原计划的1.5倍,结果提前3小时完成任务,求该工人原计划每小时检修煤气管道多少米?
相关试题

