【题目】如图,利用热气球探测器测量大楼AB的高度.从热气球P处测得大楼顶部B的俯角为37°,大楼底部A的俯角为60°,此时热气球P离地面的高度为120m.试求大楼AB的高度(精确到0.1m).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)

参考答案:
【答案】大楼AB的高度约为68.1米.
【解析】
试题分析:首先过P作PC⊥AB,垂足为C,进而求出PC的长,利用tan37°=![]() ,得BC的长,即可得出答案.
,得BC的长,即可得出答案.
试题解析:过P作PC⊥AB,垂足为C,由已知∠APC=60°,∠BPC=37°,

且由题意可知:AC=120米.
在Rt△APC中,由tan∠APC=![]() ,
,
即tan60°=![]() ,得PC=3
,得PC=3![]() =40
=40![]() .
.
在Rt△BPC中,由tan∠BPC=![]() ,
,
即tan37°=![]() ,得BC=40
,得BC=40![]() ×0.75≈51.9.
×0.75≈51.9.
因此AB=AC-BC=120-51.9=68.1,
即大楼AB的高度约为68.1米.
-
科目: 来源: 题型:
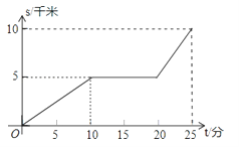
查看答案和解析>>【题目】某天早晨,王老师从家出发,骑摩托车前往学校,途中在路旁一家饭店吃早餐,如图所示的是王老师从家到学校这一过程中行驶路程s(千米)与时间t(分)之间的关系.
(1)学校离他家多远?从出发到学校,用了多少时间?
(2)王老师吃早餐用了多少时间?
(3)王老师吃早餐以前的速度快还是吃完早餐以后的速度快?最快时速达到多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC 中,D 是 BC 边的中点,E、F 分别在 AD 及其延长线上,CE∥BF,连接BE、CF.
(1)求证:△BDF ≌△CDE;
(2)若 DE =
 BC,试判断四边形 BFCE 是怎样的四边形,并证明你的结论.
BC,试判断四边形 BFCE 是怎样的四边形,并证明你的结论.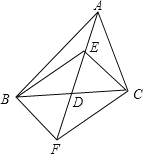
-
科目: 来源: 题型:
查看答案和解析>>【题目】青少年视力水平下降已引起全社会的广泛关注,为了解某市初中毕业年级5 000名学生的视力情况,我们从中抽取了一部分学生的视力作为样本进行数据处理,得到如下的不完整的频数分布表和频数分布直方图:
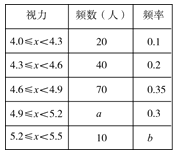
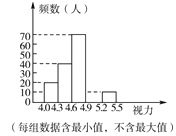
请根据以上图表信息回答下列问题:
(1)在频数分布表中,a=________,b=________;
(2)补全条形统计图;
(3)若视力在4.6以上(含4.6)均属正常,根据上述信息估计全区初中毕业生中视力正常的学生有多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某剧院的观众席的座位为扇形,且按下列分式设置:
排数(x)
1
2
3
4
…
座位数(y)
50
53
56
59
…
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
-
科目: 来源: 题型:
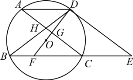
查看答案和解析>>【题目】如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及其延长线分别交AC,BC于点G,F.
(1)求证:DF垂直平分AC;
(2)若弦AD=10,AC=16,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数
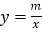 的图象的两个交点.
的图象的两个交点.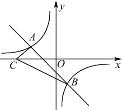
(1)求反比例函数和一次函数的解析式;
(2)若C是x轴上一动点,设t=CB-CA,求t的最大值,并求出此时点C的坐标.
相关试题

