【题目】如图,点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
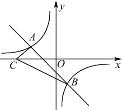
(1)求反比例函数和一次函数的解析式;
(2)若C是x轴上一动点,设t=CB-CA,求t的最大值,并求出此时点C的坐标.
参考答案:
【答案】(1)![]() ;y=-x-1;(2)
;y=-x-1;(2)![]() ;C(-5,0).
;C(-5,0).
【解析】
(1)将点B的坐标代入![]() 中求得m的值即可得到反比例函数的解析式,再将点A(-2,n)代入所得反比例函数的解析式求得n的值即可得到点A的坐标,然后将A、B两点的坐标代入一次函数的解析式列出关于k、b的方程组,解方程组求得k、b的值即可得到一次函数的解析式;
中求得m的值即可得到反比例函数的解析式,再将点A(-2,n)代入所得反比例函数的解析式求得n的值即可得到点A的坐标,然后将A、B两点的坐标代入一次函数的解析式列出关于k、b的方程组,解方程组求得k、b的值即可得到一次函数的解析式;
(2)如下图,作出点A关于x轴的对称点A′,连接BA′并延长交x轴于点C,则此时的点C为所求点,由已知条件求得直线BA′的解析式,即可由所得解析式求得点C的坐标,然后由t=CB-CA=CB-CA′即可求得所求的t的值.
(1)∵点B(1,-2)在反比例函数![]() 的图象上,
的图象上,
∴m=-2,
∴反比例函数解析式为![]() .
.
∵点A(-2,n)在反比例函数的图象上,
∴n=1,
∴A(-2,1).
由题意知![]() ,解得:
,解得:![]() ,
,
故一次函数的解析式为y=-x-1;
(2)如图,作点A关于x轴的对称点A′,连接BA′并延长交x轴于点C,则点C为所求点,

∵A(-2,1),
∴A′(-2,-1).
设直线A′B的解析式为y=mx+n,
则![]() ,解得:
,解得: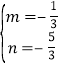 ,
,
故直线A′B的解析式为![]()
在![]() 中,令y=0,解得x=-5,则C点坐标为(-5,0),
中,令y=0,解得x=-5,则C点坐标为(-5,0),
∴BC=![]() ,A′C=
,A′C=![]() ,
,
∴此时t=CB-CA有最大值,且t最大=CB-CA′=A′B=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,利用热气球探测器测量大楼AB的高度.从热气球P处测得大楼顶部B的俯角为37°,大楼底部A的俯角为60°,此时热气球P离地面的高度为120m.试求大楼AB的高度(精确到0.1m).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
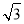 ≈1.73)
≈1.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某剧院的观众席的座位为扇形,且按下列分式设置:
排数(x)
1
2
3
4
…
座位数(y)
50
53
56
59
…
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
-
科目: 来源: 题型:
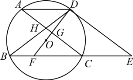
查看答案和解析>>【题目】如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及其延长线分别交AC,BC于点G,F.
(1)求证:DF垂直平分AC;
(2)若弦AD=10,AC=16,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABE和△ADC是△ABC分别沿着AB、AC边翻折180°形成的,若∠1:∠2:∠3=28:5:3,则∠α的度数为__度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点C是直线l1上一点,在同一平面内,把一个等腰直角三角板ABC任意摆放,其中直角顶点C与点C重合,过点A作直线l2⊥l1,垂足为点M,过点B作l3⊥l1,垂足为点N

(1)当直线l2,l3位于点C的异侧时,如图1,线段BN,AM与MN之间的数量关系 (不必说明理由);
(2)当直线l2,l3位于点C的右侧时,如图2,判断线段BN,AM与MN之间的数量关系,并说明理由;
(3)当直线l2,l3位于点C的左侧时,如图3,请你补全图形,并直接写出线段BN,AM与MN之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为倡导低碳生活,绿色出行,某自行车俱乐部利用周末组织“远游骑行”活动,自行车队从甲地出发,目的地乙地,自行车队出发1小时后,恰有一辆邮政车从甲地出发,沿自行车队行进路线前往乙地,到达乙地后立即按原路返回甲地.自行车队与邮政车行驶速度均保持不变,并且邮政车行驶速度是自行车队行驶速度的3倍.如图表示自行车队、邮政车离甲地的路程y(km)与自行车队离开甲地时间x(h)的关系图象,请根据图象提供的信息,回答下列问题
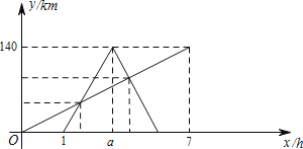
(1)自行车队行驶的速度是______;邮政车行驶速度是______;a=______;
(2)邮政车出发多少小时与自行车队首次相遇?
(3)邮政车在返程途中与自行车队再次相遇时的地点距离甲地多远?
相关试题

