搜索
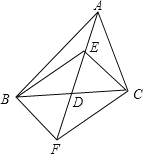
【题目】在△ABC 中，D 是 BC 边的中点，E、F 分别在 AD 及其延长线上，CE∥BF，连接BE、CF．
（1）求证：△BDF ≌△CDE；
（2）若 DE =
BC，试判断四边形 BFCE 是怎样的四边形，并证明你的结论．
参考答案：
【答案】见解析
【解析】
（1）由已知条件易得∠CED=∠BFD，BD=CD，结合∠BDF=∠CDE即可证得：△BDF≌△CDE；
（2）由△BDF≌△CDE易得DE=DF，结合BD=CD可得四边形BFCE是平行四边形，结合DE=
BC可得EF=BC，由此即可证得平行四边形BFCE是矩形.
（1）∵CE∥BF，
∴∠CED=∠BFD.
∵D是BC边的中点，
∴BD=DC，
在△BDF和△CDE中，
，
∴△BDF≌△CDE（AAS）.
（2）四边形BFCE是矩形.理由如下：
∵△BDF≌△CDE，
∴DE=DF，
又∵BD=DC，
∴四边形BFCE是平行四边形.
∵DE=BC，DE=EF，
∴BC=EF，
∴平行四边形BFCE是矩形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在公路 MN 两侧分别有 A
, A
......A
,七个工厂,各工厂与公路 MN(图中粗线)之间有小公路连接.现在需要在公路 MN 上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是（ ）.①车站的位置设在 C 点好于 B 点;
②车站的位置设在 B 点与 C 点之问公路上任何一点效果一样;
③车站位置的设置与各段小公路的长度无关.
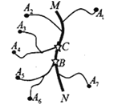
A.①B.②C.①③D.②③
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在电线杆上的C处引拉线CE、CF固定电线杆，拉线CE和地面所成的角
∠CED=60°，在离电线杆6米的B处安置测角仪AB，在A处测得电线杆上C处的仰角为30°，已知测角仪高AB为1.5米，求拉线CE的长 （结果精确到0.1米，参考数据：
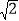≈1.414，
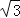≈1.732）．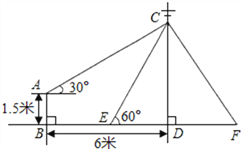
-
科目： 来源： 题型：
查看答案和解析>>【题目】直接填答案：
①（－5）＋（－5）＝______；②（－5）＋（＋8）＝______；③90
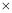（－3）＝______；④（－5）－（－3）＝______；⑤－16－8＝_____；⑥8－16＝______；
⑦
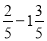＝______；⑧
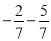＝_____。⑨
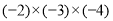＝_____；⑩
＝______。 -
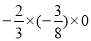科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，E、F是对角线BD上两点，且∠EAF=45°，将△ADF绕点A顺时针旋转90°后，得到△ABQ，连接EQ，求证：
（1）EA是∠QED的平分线；
（2）EF2=BE2+DF2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下面为某年11月的日历：
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
(1)在日历上任意圈出一个竖列上相邻的3个数；
①设中间的一个数为
，则另外的两个数为 、 ； ②若已知这三个数的和为42，则这三天都在星期 ；
(2)在日历上用一个小正方形任意圈出其中的9个数，设圈出的9个数的中心的数为b,若这9个数的和为153，求
的值. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知数轴上两点A、B对应的数分别为－1、3，点P为数轴上一动点，其对应的数为x．
（1）若点P到点A、点B的距离相等，求点P对应的数；
（2）数轴上是否存在点P，使点P到点A、点B的距离之和为6？若存在，请求出x的值；若不存在，说明理由．
（3）点A、点B分别以2个单位长度/分、1个单位长度/分的速度向右运动，同时点P以6个单位长度/分的速度从O点向左运动．当遇到A时，点P立即以同样的速度向右运动，并不停地往返于点A与点B之间，求当点A与点B重合时，点P所经过的总路程是多少？
相关试题
