【题目】如果正方形![]() 的边长为4,
的边长为4,![]() 为
为![]() 边上一点,
边上一点,![]() ,
,![]() 为线段
为线段![]() 上一点,射线
上一点,射线![]() 交正方形的一边于点
交正方形的一边于点![]() ,且
,且![]() ,那么
,那么![]() 的长为__________.
的长为__________.
参考答案:
【答案】![]() 或
或![]()
【解析】
因为BM可以交AD,也可以交CD.分两种情况讨论:
①BM交AD于F,则△ABE≌△BAF.推出AF=BE=3,所以FD=EC,连接FE,则四边形ABEF为矩形,所以M为该矩形的对角线交点,所以BM=AC的一半,利用勾股定理得到AE等于5,即可求解;
②BM交CD于F,则BF垂直AE(通过角的相加而得)且△BME∽△ABE,则![]() ,所以求得BM等于
,所以求得BM等于![]() .
.
分两种情况讨论:
①BM交AD于F,
∵∠ABE=∠BAF=90°,AB=BA,AE=BF,
∴△ABE≌△BAF(HL)
∴AF=BE,
∵BE=3,
∴AF=3,
∴FD=EC,
连接FE,则四边形ABEF为矩形,
∴BM=![]() AE,
AE,
∵AB=4,BE=3,
∴AE=![]() =5,
=5,
∴BM=![]() ;
;

②BM交CD于F,
∵△ABE≌△BCF,
∴∠BAE=∠CBF,
∵∠BAE+∠BEA=90°,
∴∠BEM+∠EBM=90°,
∴∠BME=90°,
即BF垂直AE,
∴△BME∽△ABE,
∴![]() ,
,
∵AB=4,AE=5,BE=3,
∴BM=![]() .
.
综上,故答案为:![]() 或
或![]()

-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按
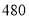 元销售时,每天可销售
元销售时,每天可销售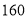 个;若销售单价每降低元,每天可多售出
个;若销售单价每降低元,每天可多售出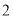 个.已知每个玩具的固定成本为
个.已知每个玩具的固定成本为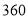 元,问这种玩具的销售单价为多少元时,厂家每天可获利润
元,问这种玩具的销售单价为多少元时,厂家每天可获利润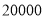 元?
元? -
科目: 来源: 题型:
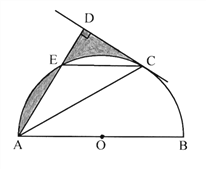
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD
 CD,垂足为D,AD交⊙O 于E,连接CE.(1)求证:CD 是⊙O 的切线
CD,垂足为D,AD交⊙O 于E,连接CE.(1)求证:CD 是⊙O 的切线(2)若E是弧AC的中点,⊙O 的半径为1,求图中阴影部分的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线
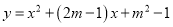 经过坐标原点,且当
经过坐标原点,且当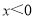 时, y随x的增大而减小.
时, y随x的增大而减小.(1)求抛物线的解析式;
(2)如下图,设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB
 x轴于点B, DC
x轴于点B, DC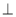 x轴于点C.
x轴于点C.①当 BC=1时,直接写出矩形ABCD的周长;
②设动点A的坐标为(a, b),将矩形ABCD的周长L表示为a的函数,并写出自变量的取值范围,判断周长是否存在最大值,如果存在,求出这个最大值,并求出此时点A的坐标;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在△ABC中,∠A
 ,P是BC边上的一点,
,P是BC边上的一点, ,
, 是点P关于AB、AC的对称点,连结
是点P关于AB、AC的对称点,连结 ,分别交AB、AC于点D、E.
,分别交AB、AC于点D、E. ①若
 ,求
,求 的度数;
的度数; ②请直接写出∠A与
 的数量关系:___________________________;
的数量关系:___________________________; (2)如图2,在△ABC中,若∠BAC
 ,用三角板作出点P关于AB、AC的对称点
,用三角板作出点P关于AB、AC的对称点 、
、 ,(不写作法,保留作图痕迹),试判断点
,(不写作法,保留作图痕迹),试判断点 ,
, 与点A是否在同一直线上,并说明理由.
与点A是否在同一直线上,并说明理由. 

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,F、G是AD边上的两个点,且FC平分∠BCD,GB平分∠ABC,FC与GB交于点E.
①AB=AG;②连接BF、CG,则四边形BFGC为等腰梯形;③AF=DG;④△ABG∽△DCF.
以上四个结论中一定成立的有( )个.

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】小强骑车从家到学校要经过一段先上坡后下坡的路,在这段路上小强骑车的距离s(千米)与骑车的时间t(分钟)之间的函数关系如图所示,请根据图中信息回答下列问题:

(1)小强去学校时下坡路长 千米;
(2)小强下坡的速度为 千米/分钟;
(3)若小强回家时按原路返回,且上坡的速度不变,下坡的速度也不变,那么回家骑车走这段路的时间是 分钟.
相关试题

